在 Python 中估计 GARCH 参数存在的问题(基于 arch 包)
本文承接前面的几篇博客,对 Python 中专门用于波动率模型分析的 arch 包进行了简单的测试,试图发现在估计 GARCH 参数时可能存在的问题。
在 Python 中估计 GARCH 参数存在的问题(基于 arch 包)
概述
前文链接:
arch 包由来自牛津大学的 Kevin Sheppard 教授设计开发,可以用于模拟、估计和预测 ARCH、GARCH、TARCH、EGARCH、RiskMetrics 等常见的波动率模型。目前的版本(4.15)只限于单变量波动率模型。
和 R 语言中类似功能的包不同,得力于 Python 对面向对象设计的出色支持,arch 以高度面向对象的方式编写,并且能清晰的看出设计模式的应用,这使得对 arch 进行自动定义扩展变得相对容易。
我在完成《Elements of Financial Risk Management (Second Edition)》课后实践习题时主要依赖的就是 arch 包,同时编写了一些自定义扩展,以实现某些目前 arch 包并不支持的模型。(项目地址:EFRMinPython)
Kevin Sheppard 教授的 Python 教程也非常推荐。
GARCH(1,1) 模型参数的设定
根据经验,GARCH(1,1) 模型的三个参数有如下几个特点:
- $\omega$ 和 $\alpha$ 通常很小,接近于 0
- $\beta$ 相对于 $\omega$ 和 $\alpha$ 来说通常很大,可能在 0.9 以上
- $\beta$ 与 $\alpha$ 的和非常接近于 1,可能在 0.95 以上
因此,和前文出现的例子不同,本文在选择的 GARCH(1, 1) 模型参数时采用了一个比较贴近现实的组合:
- $\omega = 0.1$
- $\alpha = 0.05$
- $\beta = 0.9$
简单测试 arch 包
沿用前文的思路,对 arch 包的测试分为纵向和横向两个方面:
- 纵向:测试估计值随样本数据长度的增加是否有收敛趋势
- 横向:测试估计值在中等样本量和大样本量环境下是否显现出无偏性
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from arch.univariate import ZeroMean, GARCH, Normal
import numpy as np
import pandas as pd
from scipy import stats
import seaborn as sns
rs = np.random.RandomState(123)
dist = Normal(random_state=rs)
vol = GARCH(p=1, o=0, q=1)
sim_mod = ZeroMean(volatility=vol, distribution=dist)
params = [0.1, 0.05, 0.9]
sim_data = sim_mod.simulate(params, 1000)
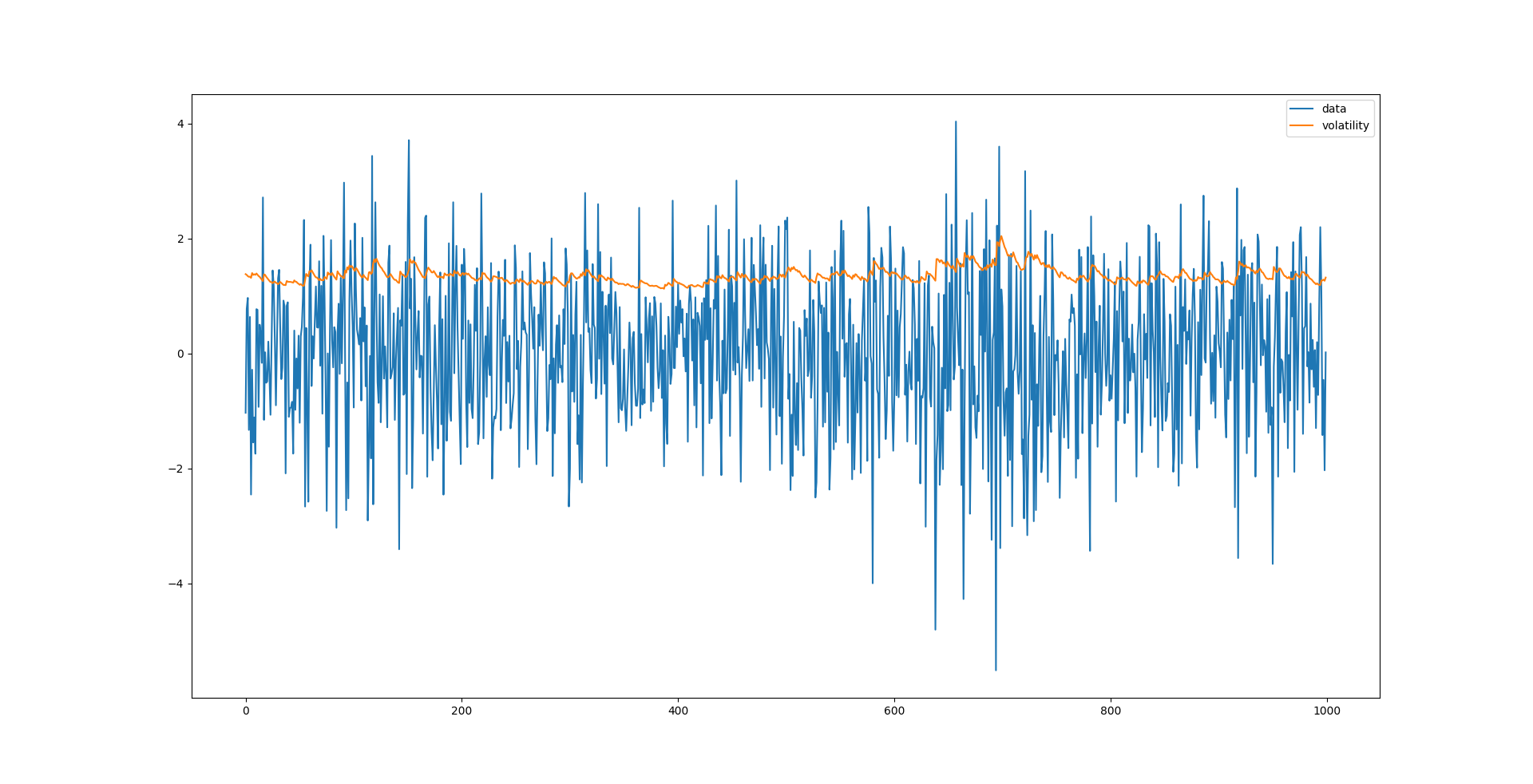
print(sim_data.head())
'''
data volatility errors
0 -1.033154 1.379696 -1.033154
1 0.775463 1.366226 0.775463
2 0.966169 1.345357 0.966169
3 -1.331714 1.332539 -1.331714
4 0.634797 1.336700 0.634797
'''
sim_data[['data', 'volatility']].plot()
在 arch 中构造一个时间序列模型对象需要将三个部分组合起来:
- 时间序列动态结构,这里采用最简单的
ZeroMean,即没有任何动态结构。复杂一点的情况可以使用ARX类提供自回归的动态结构。 - 波动率模型,这里采用的
GARCH。 - 随机项的分布,这里采用的
Normal,即正态分布。根据经验,标准化 t 分布对现实数据拟合的效果更好。
模拟数据 sim_data 包含三列,分别是 data、volatility 和 errors。data 表示最终的模拟结果,volatility 表示模拟的条件波动率,errors 表示模拟的随机项。由于采用了 ZeroMean,data 和 errors 完全一样,若采用了一个自回归模型,data 和 errors 会有很大区别。
纵向测试:收敛性
纵向测试的样本长度从 200 递增到 1000,对于三个参数来说,每次估计记录三个值,分别是估计值,95% 置信区间的上下界。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
sample_lenght = range(200, 1000)
test_omega = pd.DataFrame({
'value': 0.0,
'upper_bound': 0.0,
'lower_bound': 0.0},
index=sample_lenght)
test_alpha = pd.DataFrame({
'value': 0.0,
'upper_bound': 0.0,
'lower_bound': 0.0},
index=sample_lenght)
test_beta = pd.DataFrame({
'value': 0.0,
'upper_bound': 0.0,
'lower_bound': 0.0},
index=sample_lenght)
mul = stats.norm.ppf(0.975)
for i in sample_lenght:
fit_mod = ZeroMean(
y=sim_data['data'][0:i],
volatility=vol,
distribution=dist)
res = fit_mod.fit(disp='off')
test_omega['value'][i] = res.params['omega']
test_omega['upper_bound'][i] = res.params['omega'] + mul * res.std_err['omega']
test_omega['lower_bound'][i] = res.params['omega'] - mul * res.std_err['omega']
test_alpha['value'][i] = res.params['alpha[1]']
test_alpha['upper_bound'][i] = res.params['alpha[1]'] + mul * res.std_err['alpha[1]']
test_alpha['lower_bound'][i] = res.params['alpha[1]'] - mul * res.std_err['alpha[1]']
test_beta['value'][i] = res.params['beta[1]']
test_beta['upper_bound'][i] = res.params['beta[1]'] + mul * res.std_err['beta[1]']
test_beta['lower_bound'][i] = res.params['beta[1]'] - mul * res.std_err['beta[1]']
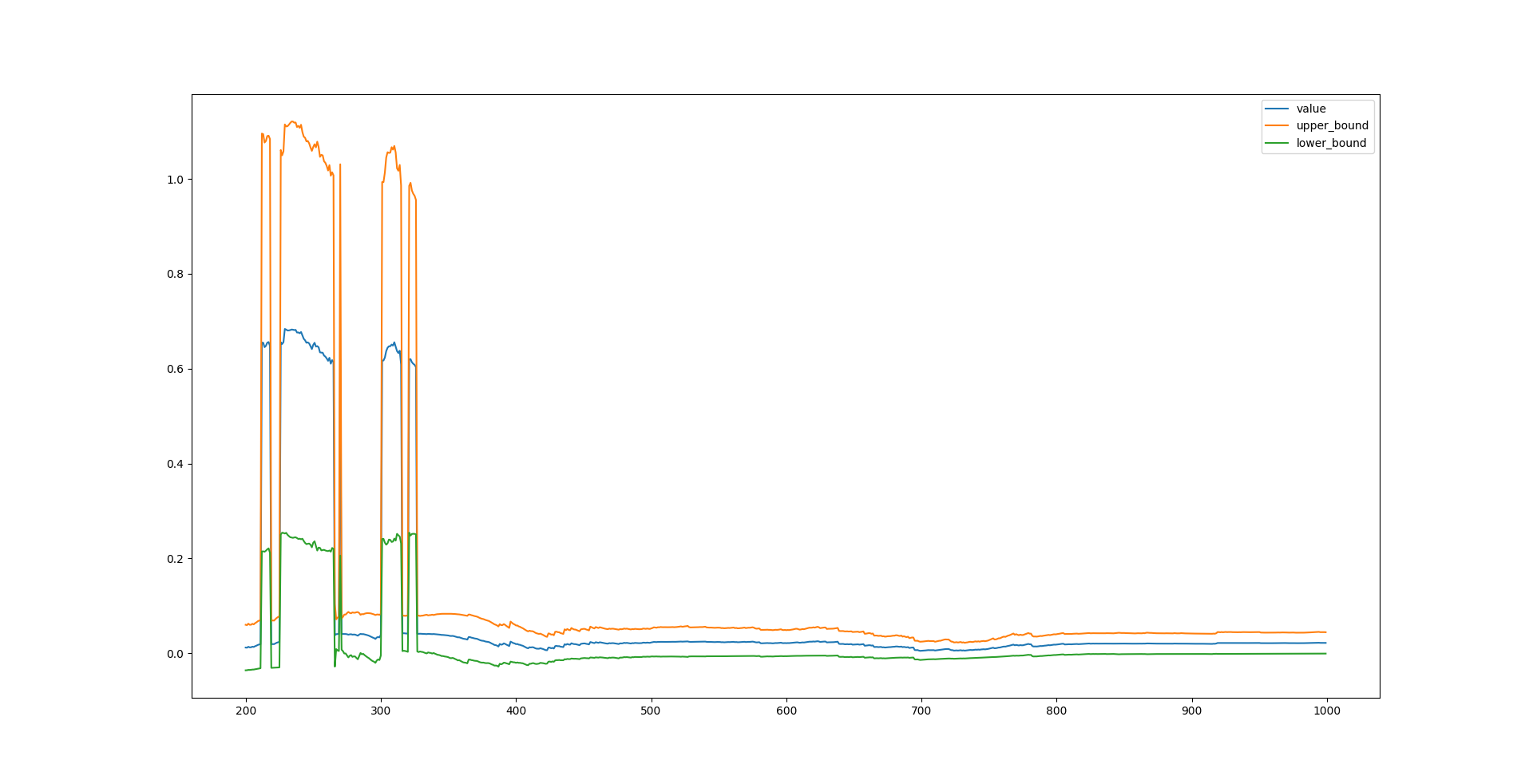
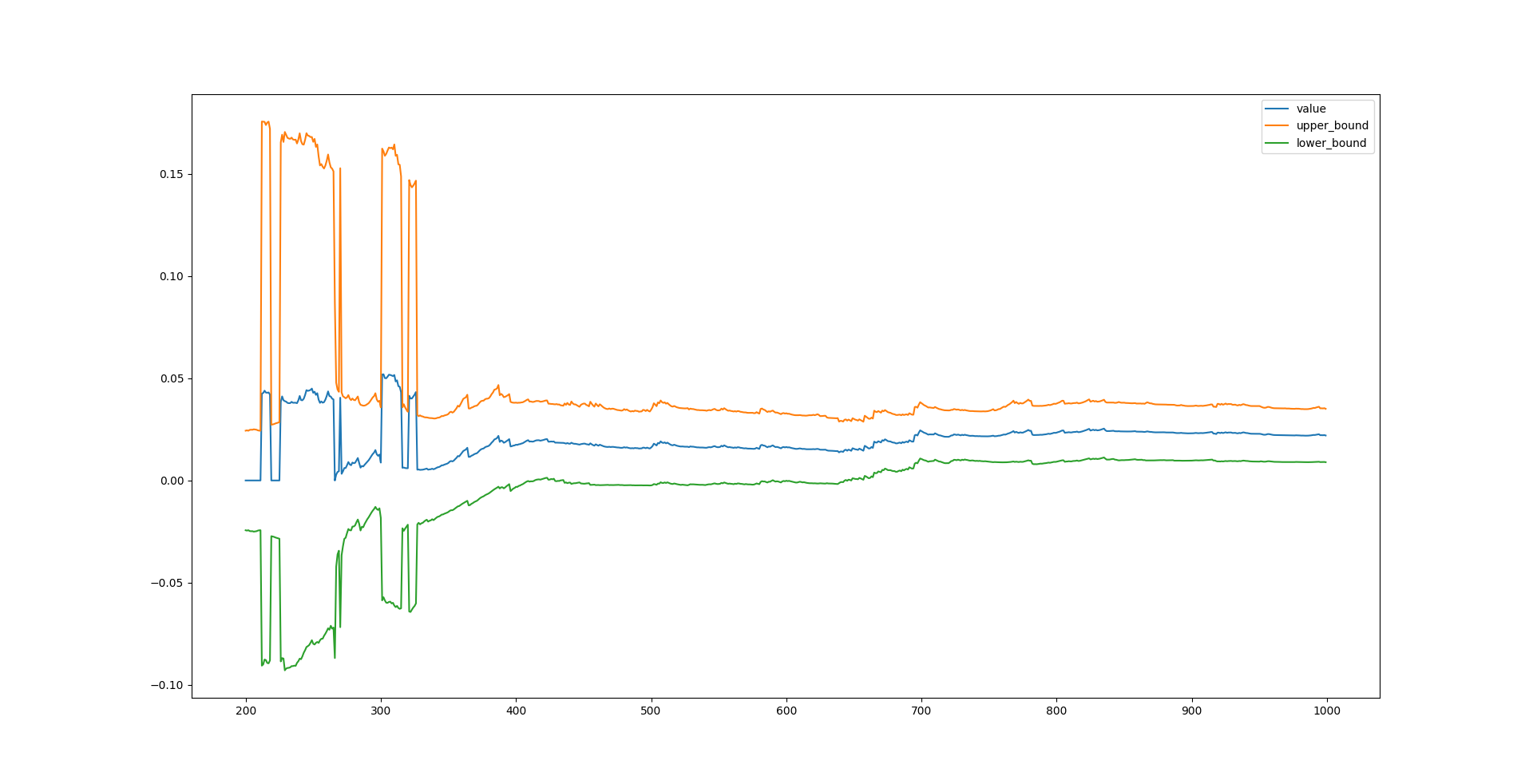
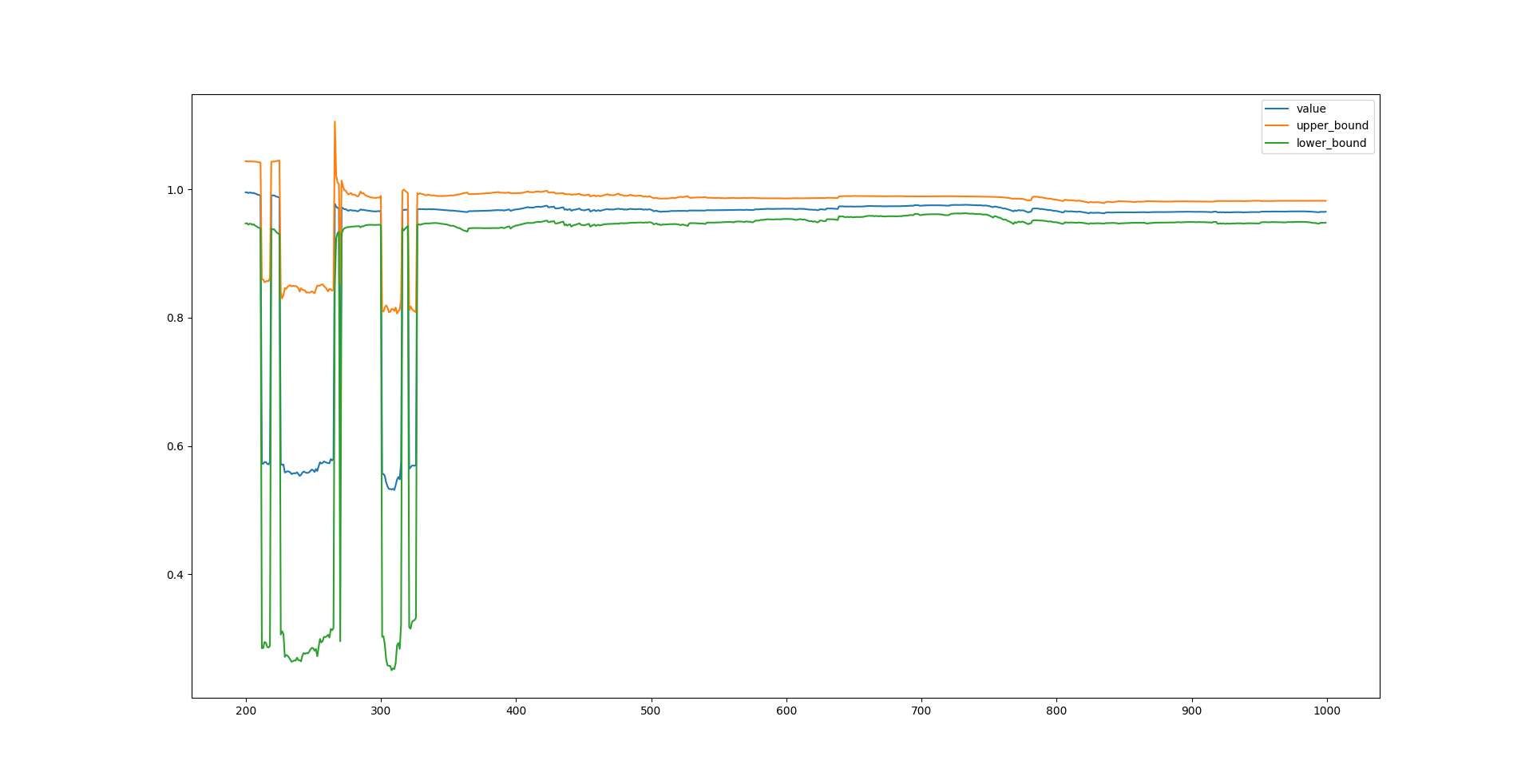
分别画出三个参数的图像:
1
test_omega.plot()
1
test_alpha.plot()
1
test_beta.plot()
在这个例子中,样本量低于 400 时,三个参数的估计都是不稳定的,尽管不稳定的结果可能是统计显著的。样本量超过 400 后,参数估计值趋于稳定,但收敛速度比较慢,即置信区间的宽度变窄的速度较慢。
最后,贴出最终估计的结果,和预设参数相比有不可忽视的差距。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
fit_mod = ZeroMean(
y=sim_data['data'],
volatility=vol,
distribution=dist)
final_res = fit_mod.fit(disp='off')
print(final_res.summary())
'''
Zero Mean - GARCH Model Results
==============================================================================
Dep. Variable: data R-squared: 0.000
Mean Model: Zero Mean Adj. R-squared: 0.001
Vol Model: GARCH Log-Likelihood: -1670.79
Distribution: Normal AIC: 3347.58
Method: Maximum Likelihood BIC: 3362.30
No. Observations: 1000
Date: Sat, Sep 05 2020 Df Residuals: 997
Time: 17:55:36 Df Model: 3
Volatility Model
=============================================================================
coef std err t P>|t| 95.0% Conf. Int.
-----------------------------------------------------------------------------
omega 0.0217 1.149e-02 1.889 5.885e-02 [-8.122e-04,4.423e-02]
alpha[1] 0.0221 6.663e-03 3.310 9.328e-04 [8.996e-03,3.512e-02]
beta[1] 0.9652 8.687e-03 111.110 0.000 [ 0.948, 0.982]
=============================================================================
Covariance estimator: robust
'''
横向测试:无偏性
从纵向测试的结果可以推测,400 可能是估计值开始稳定的样本长度下限。下面分别对样本长度是 400(中等样本量)和 1000(大样本量)两种情况测试无偏性。
样本长度是 400 的情况:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
rs = np.random.RandomState(123)
dist = Normal(random_state=rs)
sim_mod = ZeroMean(volatility=vol, distribution=dist)
test400 = pd.DataFrame({
'omega': 0.0,
'alpha': 0.0,
'beta': 0.0},
index=range(1000))
for i in test400.index:
sim_data = sim_mod.simulate(params, 400)
fit_mod = ZeroMean(
y=sim_data['data'],
volatility=vol,
distribution=dist)
res = fit_mod.fit(disp='off')
test400['omega'][i] = res.params['omega']
test400['alpha'][i] = res.params['alpha[1]']
test400['beta'][i] = res.params['beta[1]']
print(test400.head())
'''
omega alpha beta
0 0.019057 0.017495 0.969034
1 0.096857 0.080781 0.877738
2 0.083075 0.000000 0.952042
3 0.142289 0.078945 0.847505
4 0.257755 0.067600 0.817165
'''
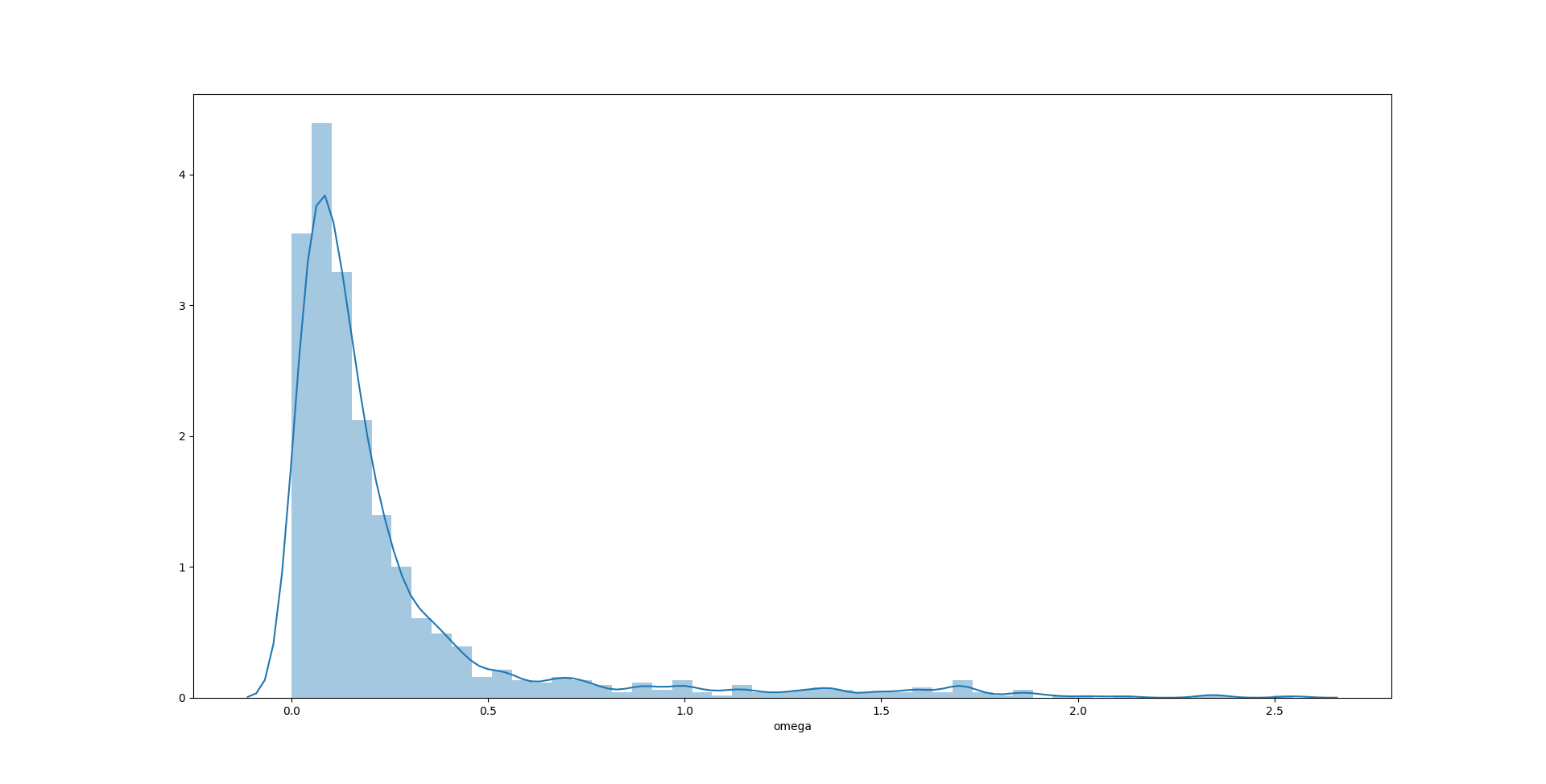
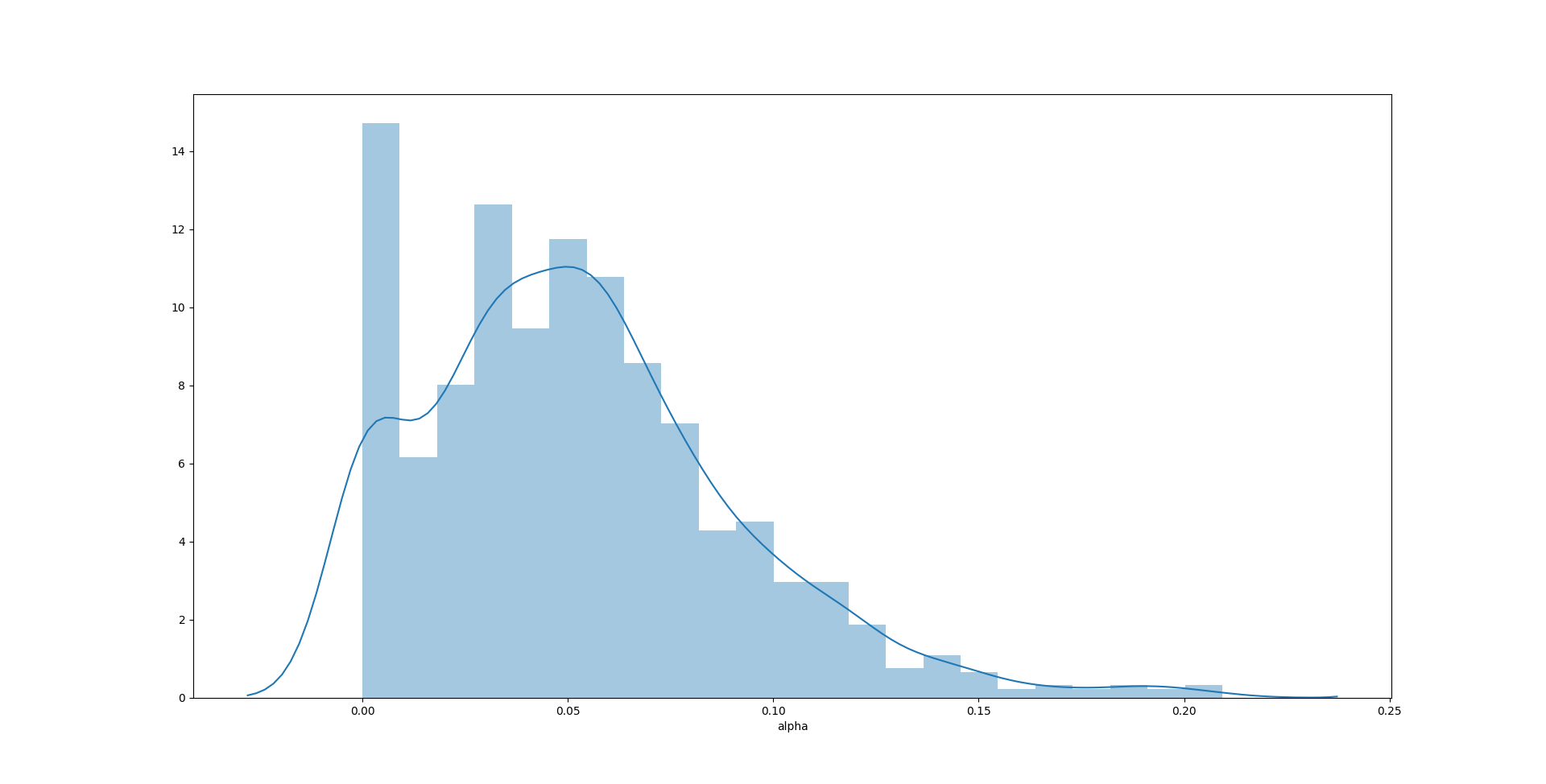
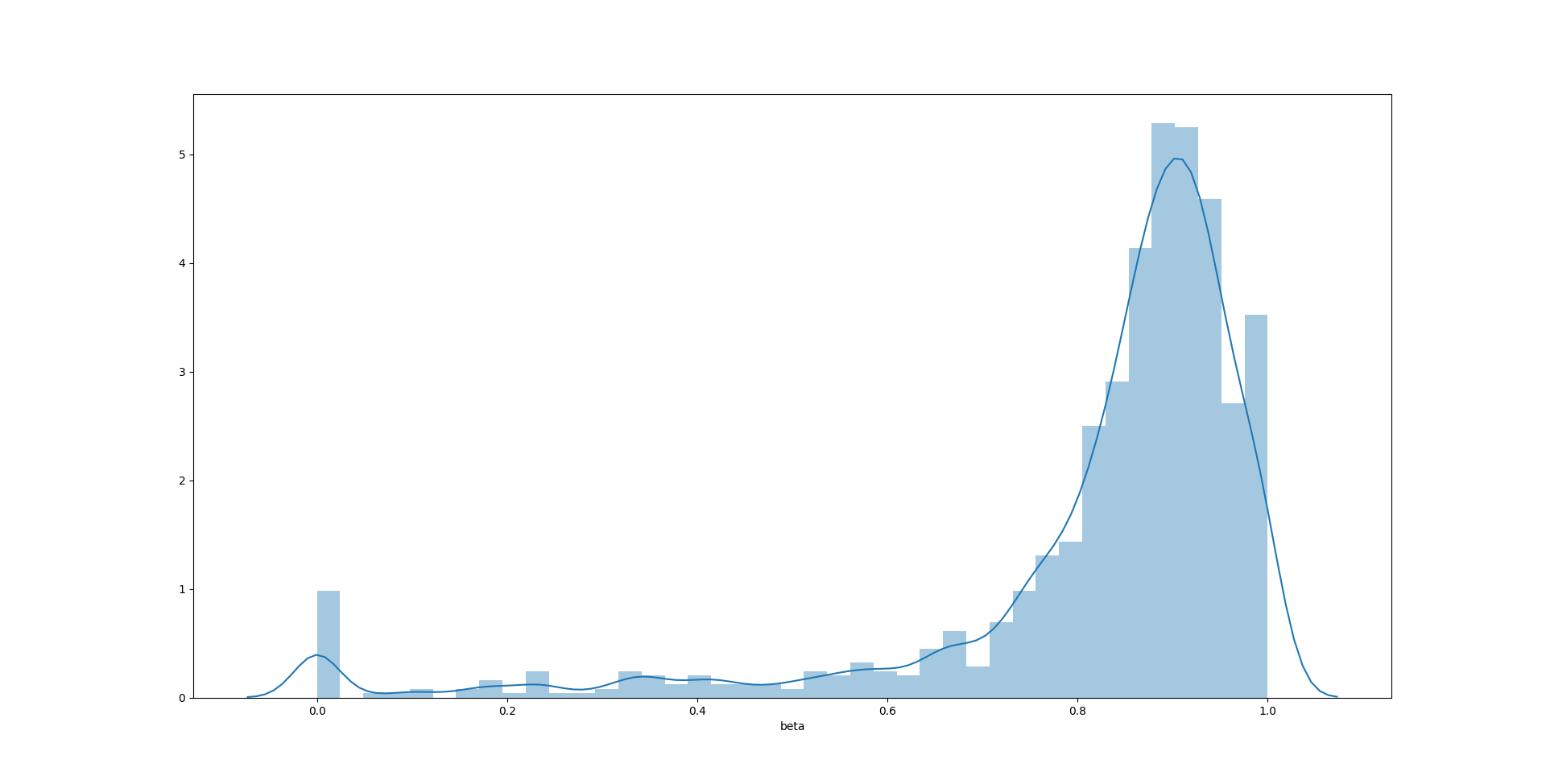
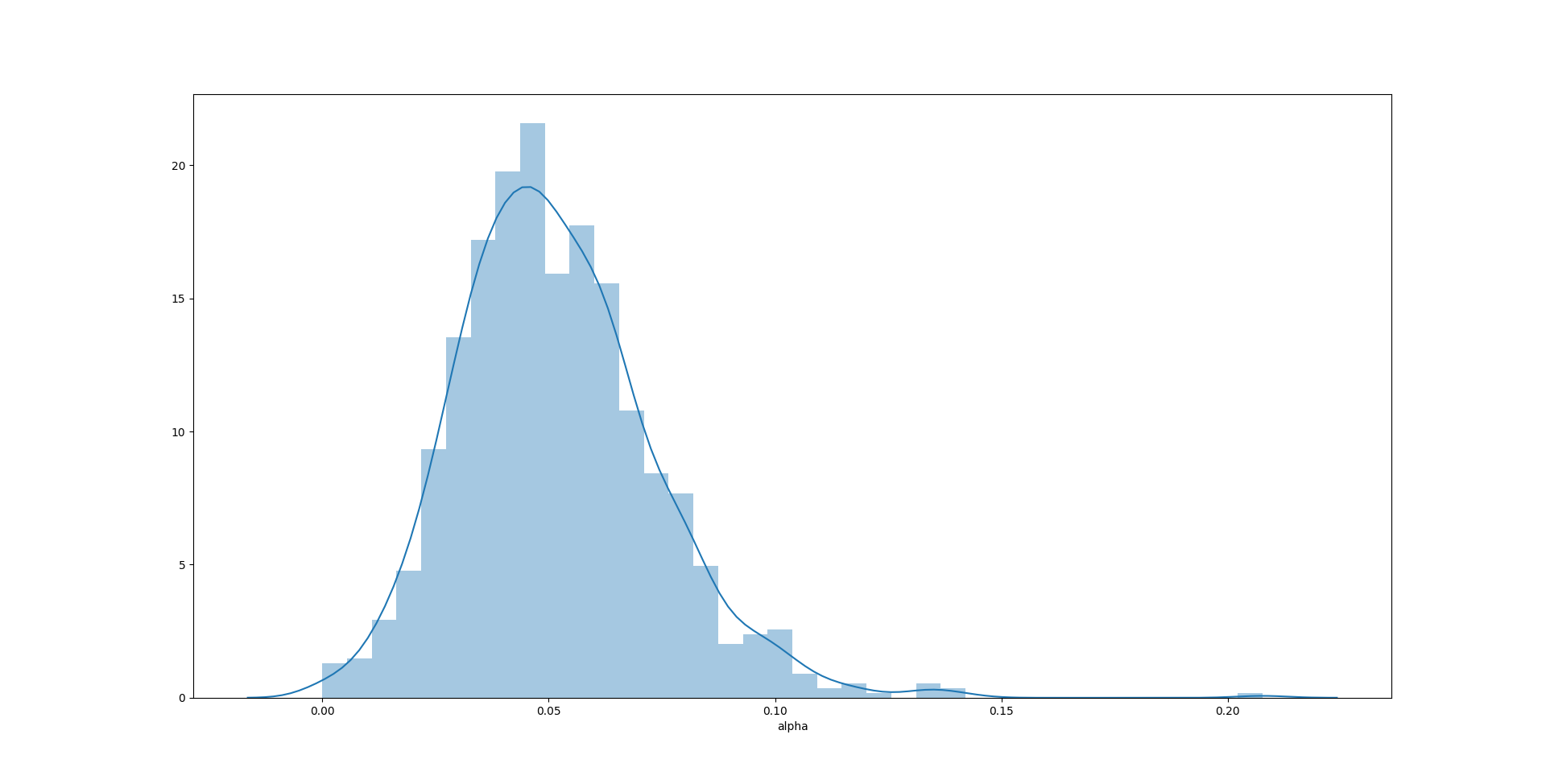
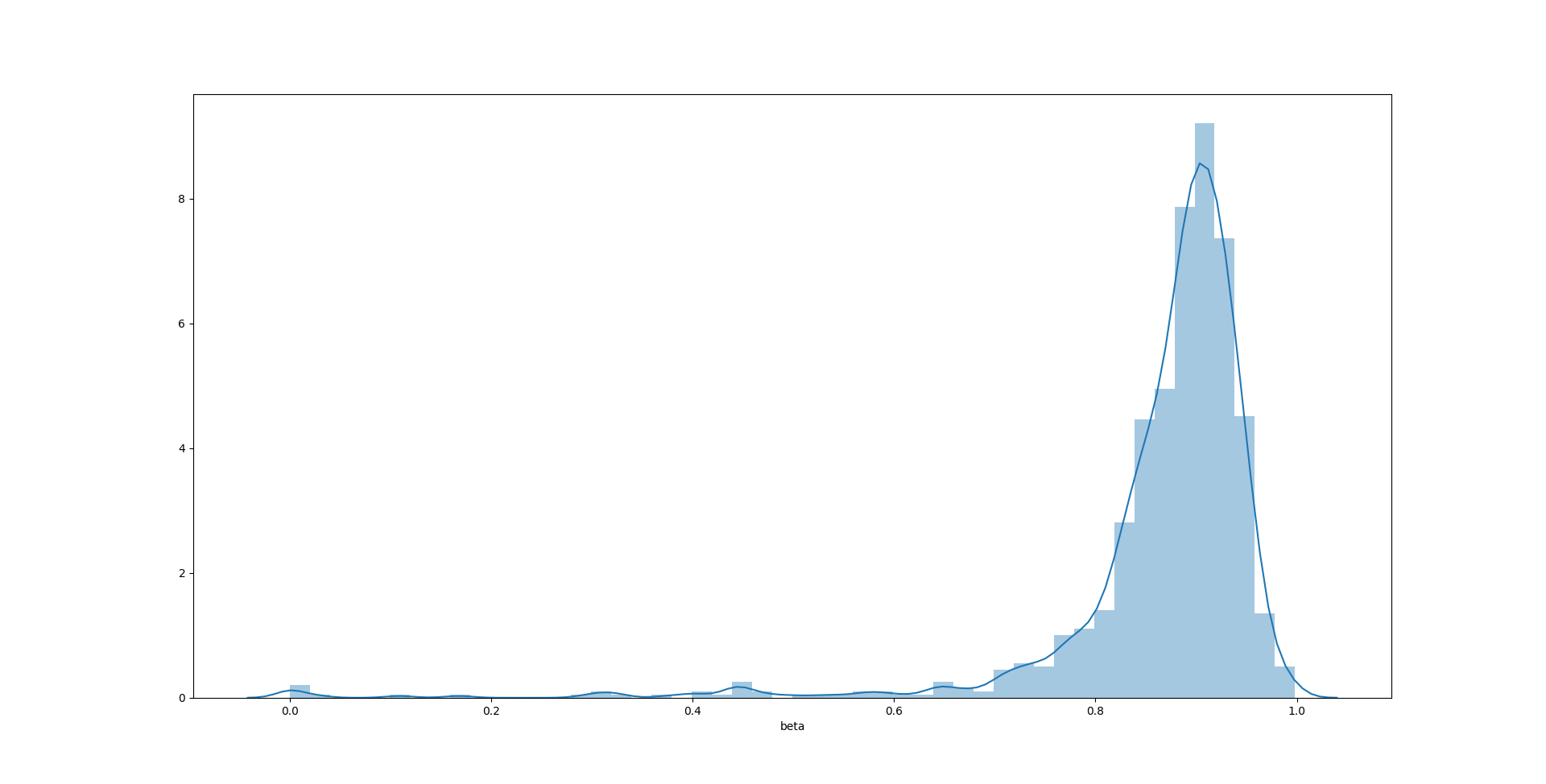
分别画出三个参数的直方图:
1
sns.distplot(test400['omega'])
1
sns.distplot(test400['alpha'])
1
sns.distplot(test400['beta'])
1
2
3
4
5
6
7
8
9
10
11
12
13
print(test400.describe())
'''
omega alpha beta
count 1000.000000 1000.000000 1000.000000
mean 0.251043 0.052557 0.820583
std 0.363563 0.038081 0.201176
min 0.000000 0.000000 0.000000
25% 0.066169 0.025913 0.806572
50% 0.128285 0.049720 0.881787
75% 0.254835 0.073094 0.929768
max 2.547629 0.209282 1.000000
'''
在这个例子中,$\alpha$ 的无偏性相对其他两个参数来说比较好,分布也最接近对称形态。$\omega$ 和 $\beta$ 的无偏性表现要差一些,主要原因可能是“尾部”太长——有一定比例的极端值出现,破坏了无偏性。$\beta$ 的估计值甚至在 0 附近出现了聚集。
样本长度是 1000 的情况:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
rs = np.random.RandomState(123)
dist = Normal(random_state=rs)
sim_mod = ZeroMean(volatility=vol, distribution=dist)
test1000 = pd.DataFrame({
'omega': 0.0,
'alpha': 0.0,
'beta': 0.0},
index=range(1000))
for i in test1000.index:
sim_data = sim_mod.simulate(params, 1000)
fit_mod = ZeroMean(
y=sim_data['data'],
volatility=vol,
distribution=dist)
res = fit_mod.fit(disp='off')
test1000['omega'][i] = res.params['omega']
test1000['alpha'][i] = res.params['alpha[1]']
test1000['beta'][i] = res.params['beta[1]']
print(test1000.head())
'''
omega alpha beta
0 0.021710 0.022056 0.965226
1 0.151901 0.036570 0.882834
2 0.151628 0.061338 0.855828
3 0.049992 0.029788 0.945866
4 0.184434 0.061361 0.848065
'''
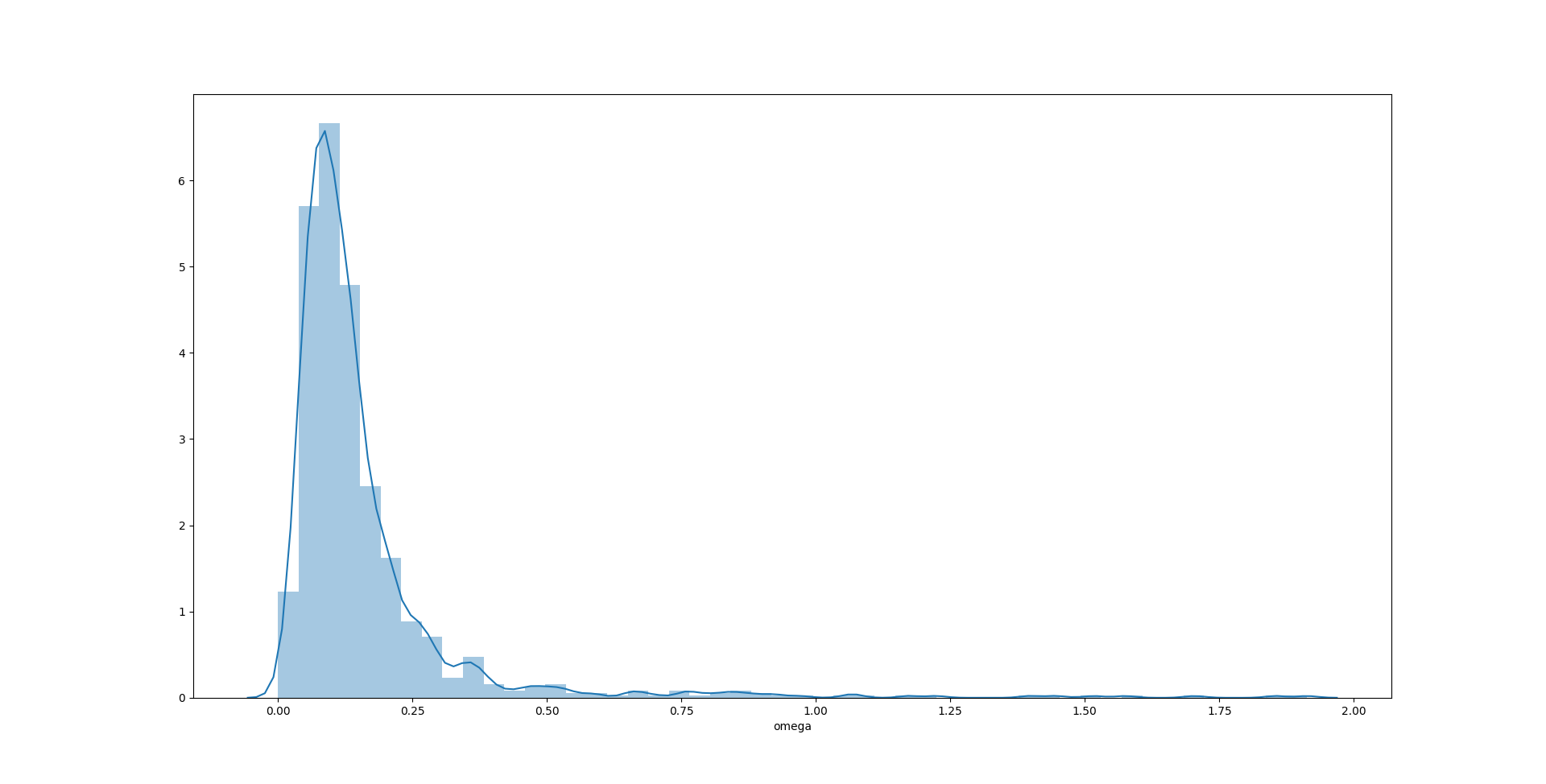
分别画出三个参数的直方图:
1
sns.distplot(test1000['omega'])
1
sns.distplot(test1000['alpha'])
1
sns.distplot(test1000['beta'])
1
2
3
4
5
6
7
8
9
10
11
12
13
print(test1000.describe())
'''
omega alpha beta
count 1.000000e+03 1000.000000 1000.000000
mean 1.584124e-01 0.051761 0.867677
std 1.879844e-01 0.021932 0.110932
min 4.840027e-09 0.000000 0.000000
25% 7.386509e-02 0.036754 0.850473
50% 1.108213e-01 0.049110 0.893345
75% 1.684538e-01 0.064596 0.920690
max 1.912558e+00 0.207638 0.998189
'''
在这个例子中,$\alpha$ 的无偏性依然是三个参数里最好的,分布也更加接近对称形态。$\omega$ 和 $\beta$ 的无偏性表现有所提高,估计值更加集中,但是还是无法杜绝极端值的出现。
直觉上看,arch 包的表现似乎略强于 rugarch 包。
arch 包如何估计参数?
以我对源代码的理解,我推测 arch 包在估计参数时采用了“模板方法模式”和“策略模式”。
想简单了解“模板方法模式”和“策略模式”请看《Head First 设计模式》读书笔记
首先,时间序列动态结构的派生类负责根据自身的结构拆解出残差项(时间序列动态结构的基类是 ARCHModel),残差项再由波动率模型和随机项分布配合计算出模型的对数似然函数(这是策略模式部分),最后对数似然函数在基类 ARCHModel 的 fit 方法中作为优化的对象,进而计算出所有模型参数(典型的模板方法模式案例,派生类提供特定组件,基类统一处理这些组件)。
ARCHModel 的 fit 方法是最终进行参数估计的地方,它所才用的计算引擎是 scipy 包里面的 SLSQP 方法。遗憾的是,尽管 scipy 中有许多可用引擎,目前版本中计算引擎却是固定的,不可自定义。
源代码片段:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func = self._loglikelihood
args = (sigma2, backcast, var_bounds)
ineq_constraints = constraint(a, b)
from scipy.optimize import minimize
options = {} if options is None else options
options.setdefault("disp", disp_flag)
opt = minimize(
func,
sv,
args=args,
method="SLSQP",
bounds=bounds,
constraints=ineq_constraints,
tol=tol,
callback=_callback,
options=options,
)
最优化计算中起始值的选择很重要,尤其是对于波动率模型来说,具体原因可以查看之前的几篇博客。为处理这个问题,arch 包提供了一项非常妙的设计——自动选择起始值,即 VolatilityProcess 类(这是所有波动率模型的基类)的 starting_values(基类中的 starting_values 是个抽象方法,没有具体实现;起始值也可以自定义)。GARCH 类中的该方法遍历了一组参数组合,从中选出对数似然值最大的组合作为起始值。
源代码片段:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def starting_values(self, resids: NDArray) -> NDArray:
p, o, q = self.p, self.o, self.q
power = self.power
alphas = [0.01, 0.05, 0.1, 0.2]
gammas = alphas
abg = [0.5, 0.7, 0.9, 0.98]
abgs = list(itertools.product(*[alphas, gammas, abg]))
target = np.mean(abs(resids) ** power)
scale = np.mean(resids ** 2) / (target ** (2.0 / power))
target *= scale ** (power / 2)
svs = []
var_bounds = self.variance_bounds(resids)
backcast = self.backcast(resids)
llfs = np.zeros(len(abgs))
for i, values in enumerate(abgs):
alpha, gamma, agb = values
sv = (1.0 - agb) * target * np.ones(p + o + q + 1)
if p > 0:
sv[1 : 1 + p] = alpha / p
agb -= alpha
if o > 0:
sv[1 + p : 1 + p + o] = gamma / o
agb -= gamma / 2.0
if q > 0:
sv[1 + p + o : 1 + p + o + q] = agb / q
svs.append(sv)
llfs[i] = self._gaussian_loglikelihood(sv, resids, backcast, var_bounds)
loc = np.argmax(llfs)
return svs[int(loc)]
几点启发
无论是 arch 还是 rugarch,参数估计都是基于极大似然法,并且高度依赖数值最优化算法的选择和微调。因此,可以推测估计结果偶然出现极端值的现象可能是该框架的通病,如果要突破这一问题的话可能需要改变参数估计的方法论,例如,
- 使用贝叶斯方法——bayesGARCH 包
- 使用机器学习算法——《矩估计遇到神经网络》
- 使用交叉验证的技巧
无论用那种软件和算法做参数估计,都建议提前进行纵向和横向的测试,一方面大致了解稳定估计的样本量下限是多少,另一方面大致了解估计参数的真实分布情况,用来帮助自己分析一下到底是模型不合适,还是自己运气不好。
做好计量经济学的实证分析还是要碰点儿运气的,如果运气不好,软件计算的结果不支持自己的观点,一个好想法可能就要被埋没了。
现实中的风险管理和量化交易大量依赖参数估计计算,而软件计算出的结果几乎从未被人质疑过,这里面潜藏了大量的风险。