市场收益率预期与远期收益率

著：Antti Ilmanen 译：徐瑞龙

Market’s Rate Expectations and Forward Rates

市场收益率预期与远期收益率

INTRODUCTION

引言

Our recent report Overview of Forward Rate Analysis introduced a series on the theme Understanding the Yield Curve. It argued that three main forces determine the term structure of forward rates: the market’s rate expectations; required bond risk premia; and the convexity bias. Separate reports discuss each of these forces. This report focuses on the impact of the market’s rate expectations on the yield curve shape.

我们最近的报告《远期收益率分析概述》引出了《理解收益率曲线》系列的主题。三个主要因素决定远期收益率的期限结构：市场的收益率预期、债券风险溢价和凸度偏差，这些因素将由单独的报告讨论。本报告重点关注市场收益率预期对收益率曲线形状的影响。

The impact of rate expectations on today’s yield curve shape is best isolated by assuming that the pure expectations hypothesis holds. According to this hypothesis, all government bonds have the same near-term expected return (that is, all bond risk premia are zero). If the near-term expected returns are equal across maturities, initial yield differences must offset any expected capital gains or losses that are caused by the market’s rate expectations. For example, if the market expects rates to rise and the long-term bonds to suffer capital losses, these bonds must have an initial yield advantage over the one-period bond (to offset the expected capital losses). Therefore, expectations of rising rates tend to make today’s yield curve upward sloping. Conversely, expectations of declining future rates tend to make today’s yield curve inverted. In a similar way, the market’s expectations of future curve flattening or steepening influence the curvature of today’s yield curve.

要解释收益率预期对当前收益率曲线形状的影响最好假定完全预期假说成立。根据这个假说，所有政府债券具有相同的近期预期回报（即所有债券风险溢价为零）。如果不同期限债券的近期预期回报相等，那么初始收益率差异必须抵消由市场收益率预期造成的任何预期资本损益。例如，如果市场预期收益率上升，长期债券遭受资本损失，这些债券必须比一（年）期债券具有初始收益率优势（以抵消预期的资本损失）。因此，对收益率上升的预期往往会使当前的收益率曲线向上倾斜。相反，对未来收益率下降的预期往往使当前的收益率曲线倒挂。同样的逻辑，市场对未来曲线变平或变陡的预期影响当前收益率曲线的曲率。

We emphasize the distinction between the statements “the forwards imply rising spot rates” and “the market expects rising spot rates”. The first statement is related to the forward rates’ role as break-even levels of future spot rates. By construction, the spot rate changes that the forwards imply for the next period are such rate changes that would make all government bonds earn the same one-period return. Whenever the spot rate curve is upward sloping, the forwards imply rising rates. That is, rising rates are needed to offset long-term bonds’ yield advantage. However, it does not necessarily follow that the market expects rising rates. An upward-sloping spot rate curve also may reflect higher near-term required returns for long-term bonds than for the riskless one-period bond (so-called positive bond risk premia). The changes in spot rates that the forwards imply would be approximately equal to the expected spot rate changes only if the restrictive pure expectations hypothesis were true.

我们强调“远期收益率隐含即期收益率的上升”和“市场预期即期收益率上升”之间的区别。第一种说法与远期收益率作为未来即期收益率的盈亏平衡水平有关。远期收益率所隐含的即期收益率的变化量，将使所有政府债券在同期赚取相同的回报。当即期收益率曲线向上倾斜时，远期收益率意味着收益率上升。也就是说，收益率上升以抵消长期债券的收益率优势。然而，并不一定意味着市场预期收益率上升。向上倾斜的即期收益率曲线也可能反映了近期长期债券比无风险一（年）期债券更高的短期回报（所谓正的债券风险溢价）。只有当限制性完全预期假说为真时，远期收益率隐含的即期收益率变化将近似等于预期即期收益率的变化。

In this report, we also present empirical evidence about rate expectations and conclude that the pure expectations hypothesis is, in many ways, at odds with historical experience. We show that forward rates are poor predictors of future spot rates. In fact, long-term rates tend to move away from the direction implied by the forward rates. We also contrast the expectations “implied” in the forward rate structure to the expectations revealed in explicit surveys among bond market participants. The comparison suggests that forward rates are upward-biased measures of the market’s rate expectations because the market appears to require higher expected returns for long-term bonds than for short-term bonds.

在本报告中我们还给出了关于收益率预期的实证证据，并得出结论，完全预期假说在许多方面与历史经验不一致。我们指出远期收益率不能很好地预测未来即期收益率。事实上，长期收益率往往偏离远期收益率所隐含的方向。我们还将远期收益率结构中“隐含”的预期与债券市场参与者调查中披露的预期进行了对比。比较表明远期收益率对市场收益率预期的预测是高估的，因为市场似乎要求长期债券比短期债券要有更高的预期回报。

ALGEBRAIC RELATIONS BETWEEN SPOT AND FORWARD RATES

即期收益率与远期收益率的代数关系

This section reviews the relations between spot rates and forward rates and describes forward rates’ role as break-even rates. The discussion in this section overlaps —— but expands on —— the discussion in Overview of Forward Rate Analysis. Readers familiar with the basic concepts in forward rate analysis may wish to move directly to the section “The Expectations Hypothesis and the Yield Curve.”

本节回顾即期收益率和远期收益率之间的关系，并描述远期收益率作为盈亏平衡收益率的作用。本节中的讨论与《远期收益率分析概述》中的讨论重叠，但有进一步扩展。熟悉远期收益率分析中的基本概念的读者可能希望直接跳到“预期假说和收益率曲线”部分。

Computation of Forward Rates

计算远期收益率

A spot rate is the discount rate of a single future cash flow such as a zero-coupon bond (zero). A coupon bond can be viewed and valued as a bundle of zeros. Given the price $P_n$ of an n-year zero, the annualized n-year spot rate $s_n$ can be computed as in Equation (1):¹

即期收益率是单个未来现金流的折现率，例如零息债券。付息债券可以看作是一系列零息债券的和。给定n年期零息债券的价格$P_n$，可以如等式（1）中计算年化的n年期即期收益率$s_n$：

\[P_n = \frac{100}{(1+s_n)^n}. \tag{1}\]

A forward rate is the interest rate for a loan between any two future dates, contracted today. The rate may be explicit in the price of a traded forward contract or it may be implicit in today’s spot rate curve. A zero’s discount rate (a multiyear spot rate) can be decomposed into a product of one-year forward rates. Thus, the spot rate is a geometric average of one-year forward rates:²

远期收益率是指当下约定的任何两个未来日期之间的贷款收益率。收益率可能在远期合约的价格中确定，或者可能隐含在当前的即期收益率曲线中。零息债券的贴现率（多年期即期收益率）可以分解为一系列一年期远期收益率的乘积。因此，即期收益率是一年期远期收益率的几何平均数：

\[(1+s_n)^n = (1+f_{0,1})(1+f_{1,2})(1+f_{2,3}) \cdots (1+f_{n-1,n}), \tag{2}\]

where $f_{n-1,n}$ is the one-year forward rate between maturities n-1 and n, and $f_{0,1}=s_1$. If only one spot rate is known, all forward rates cannot be computed. However, if spot rates are known for each maturity, a given term structure of spot rates implies a specific term structure of forward rates. For example, if the m-year and n-year spot rates are known, $f_{m,n}$ (the annualized n-m year rate m years forward) can be computed as in Equation (3):

其中$f_{n-1,n}$是期限n-1和n之间的一年期远期收益率，$f_{0,1}=s_1$。如果只有一个即期收益率已知，则不能计算所有的远期收益率。然而，如果每个期限的即期收益率已知，则给定即期收益率的期限结构隐含着特定的远期收益率期限结构。例如，如果m年和n年即期收益率是已知的，则可以如等式（3）中计算$f_{m,n}$（m年后的年化n-m年期远期收益率）：

\[(1+f_{m,n})^{n-m} = \frac{(1+s_n)^n}{(1+s_m)^m}. \tag{3}\]

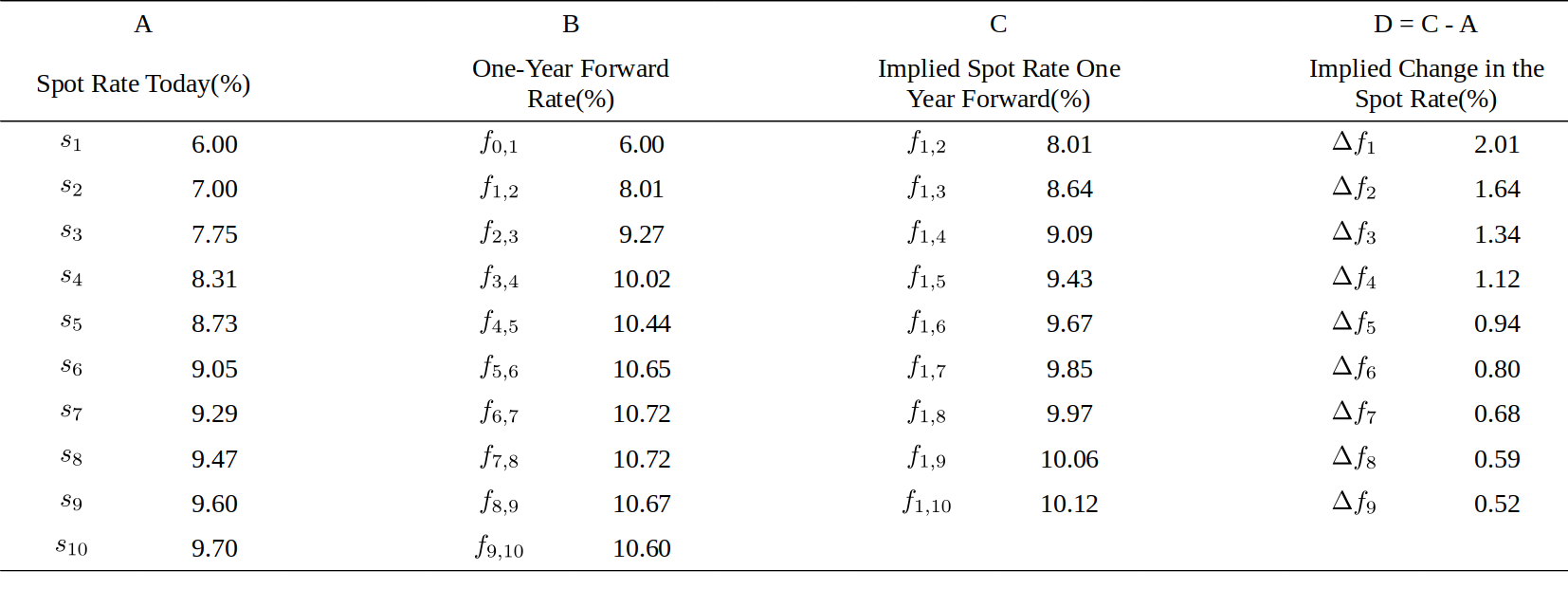
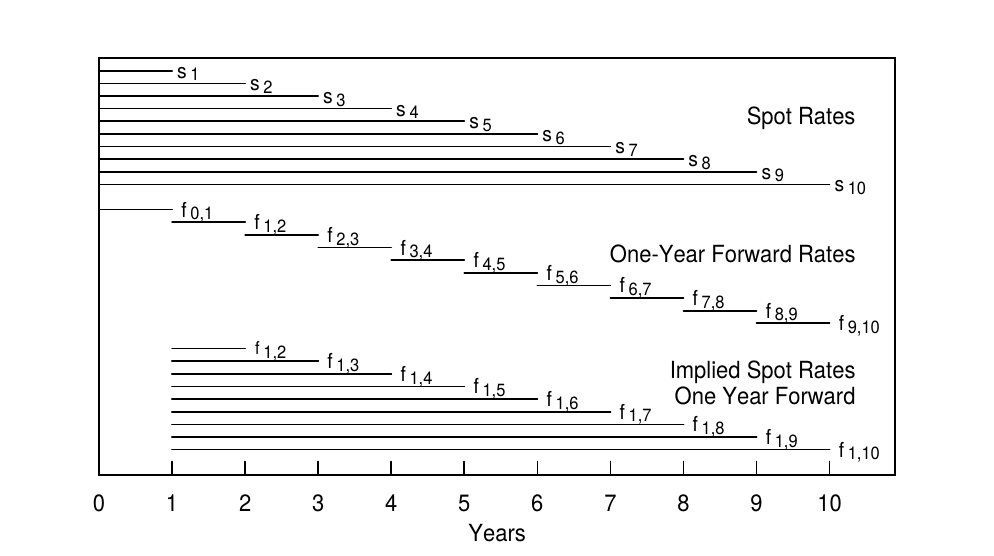
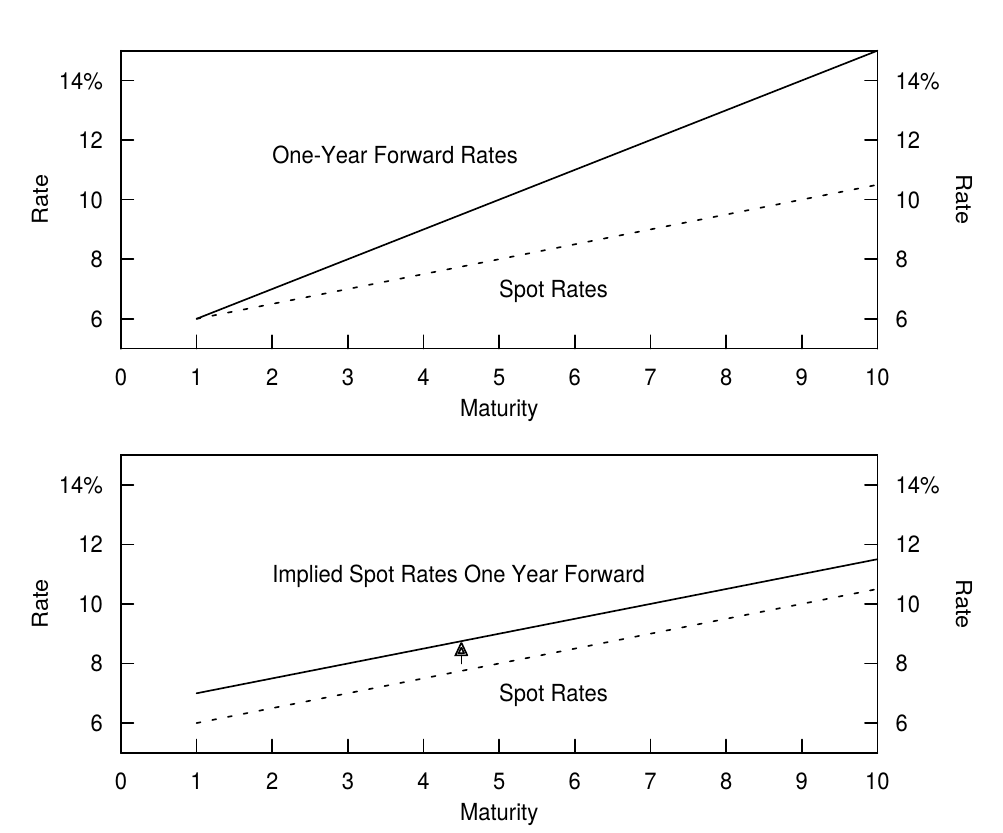
Figure 1 presents a hypothetical spot rate curve and two series derived using Equation (3): the implied forward path of the constant-maturity one-year rate at various future dates and the implied spot curve at one future date, one year hence.³ It is important to distinguish the curve of one-year forward rates in column B from the implied spot rate curve one year forward in column C. Unfortunately the terminology varies because both are sometimes called the forward curves. To clarify the relations between these curves, Figure 2 shows the future years covered by ten spot rates ($s_1$ to $s_{10}$), ten one-year forward rates ($f_{0,1}$ to $f_{9,10}$) and nine implied spot rates one year forward ($f_{1,2}$ to $f_{1,10}$). The three curves are shown graphically in Figures 3 and 4.

图1给出了一个假设的即期收益率曲线和使用等式（3）得出的两个序列：未来不同日期的一年期远期收益率的路径，以及一年后的隐含即期收益率曲线。重要的是区分B列中的一年期远期收益率曲线与C列中的一年后的隐含即期收益率曲线。遗憾的是有时两者都被称为远期收益率曲线。为了阐明这些曲线之间的关系，图2显示了未来几年10个即期收益率（$s_1$到$s_{10}$），10个一年期远期收益率（$f_{0,1}$到$f_{9,10}$）和9个一年后的隐含即期收益率（$f_{1,2}$到$f_{1,10}$）。这三条曲线分别在图3和图4中。

Figure 1. Spot Curve. Curve of One-Year Forward Rates and Implied Spot Curve One Year Forward

Figure 2. Future Years Covered by Each Rate

Forwards as Break-Even Rates

远期收益率做为盈亏平衡收益率

The numbers in column D in Figure 1 —— the difference between the implied spot curve one year forward and today’s spot curve —— show that “the forwards imply rising rates.” How should this statement be interpreted? It does not necessarily mean that the market expects rising rates. Instead, the forwards tell how much the spot curve needs to change over the next year to make all bonds earn the same holding-period return. Recall that the holding-period return is a sum of a bond’s initial yield and its capital gains or losses caused by yield changes. For example, if today’s spot curve is upward sloping, longer-term bonds have a yield advantage over the one-period bond. To equate holding-period returns across bonds, longer bonds have to suffer capital losses that offset their initial yield advantage. Forwards show exactly how much long-term rates have to increase to cause such capital losses. Stated in terms of rate levels instead of rate changes, the implied spot rates one year forward (column C in Figure 1) are such future spot rates that would make all government bonds earn the same holding-period return over the next year. (Moreover, this same return must be the return of the one-year zero because it is already known today.) This break-even relation follows from Equation (3) by setting m = 1 and rearranging:

图1中的D列中的数字——一年后的隐含即期收益率曲线与当前即期收益率曲线之间的差异——表明“远期收益率隐含着收益率上升”。应该如何解释这种说法？这并不一定意味着市场预期收益率上升。相反，远期收益率告诉我们，明年即期收益率曲线需要改变多少，以使所有债券获得相同的持有期回报。回想一下，持有期回报是债券的初始收益率与其收益率变化所造成的资本收损益之和。例如，如果当前的即期收益率曲线向上倾斜，长期债券相对于一（年）期债券具有收益率优势。为了使债券持有期回报相等，较长期的债券必须承受资本损失以抵消其最初的收益率优势。远期收益率显示了长期收益率必须增加多少以造成这种资本损失。根据收益率水平而不是收益率变化，隐含的一年后即期收益率（图1中的C列）将使所有政府债券在下一年获得相同的持有期回报。（此外，这一回报必须是一年期零息债券的回报，因为它是当前已知的。）通过设置m = 1并重新排列，从等式（3）得到：

\[\frac{(1+s_n)^n}{(1+f_{1,n})^{n-1}} = 1+s_1 . \tag{4}\]

The left-hand side of Equation (4) is the return of buying an n-year zero at rate $s_n$ today and selling it a year later at rate $f_{1,n}$. The right-hand side is the riskless return of the one-year zero. Thus, $f_{1,n}$ is the selling rate at which the n-year zero’s holding-period return equals the return of the riskless asset. A numerical example illustrates the computation of the break-even rate $f_{1,2}$. The numbers are from Figure 1: a 6% one-year spot rate and a 7% two-year spot rate. Over the next year, the return of a one-year zero is known to be 6%, while the holding-period return of a two-year zero depends on its selling price at the end of the year —— when its remaining maturity is one year. So, the question is: “What should the one-year spot rate be one year hence to make the longer zero’s holding-period return 6%?” A little math shows that the answer is 8.01%. At this selling rate, the longer zero’s price would rise from 87.34 ($= 100/(1.07^2)$) to 92.58 ($= 100/1.0801$), earning it 6% ($= 92.58/87.34 - 1$). Thus, the implied one-year spot rate one year forward, $f_{1,2}$ = 8.01%, is the level of future one-year rate that would make investors ex post indifferent to holding either of the two zeros.

等式（4）的左边是当前以$s_n$的收益率买入n年期零息债券并且在一年后以收益率$f_{1,n}$卖出所产生的回报。右边是一年期零息债券的无风险回报。因此，$f_{1,n}$是使n年期零息债券持有期回报等于无风险资产回报率的卖出收益率。示例说明了盈亏平衡收益率$f_{1,2}$的计算。数字来自图1：6％是一年期即期收益率，7％是两年期即期收益率。在下一年，一年期零息债券的收益率为6％，而两年期零息债券的收益率取决于年底的价格。所以，问题是：“一年后的即期收益率应为多少，从而使期限较长的零息债券持有期回报等于6％？”数学计算表明，答案是8.01％。在这个收益率卖出，期限较长的零息债券的价格将从87.34（$= 100/(1.07^2)$）上升到92.58（$= 100/1.0801$），获得回报6％（$= 92.58/87.34 - 1$）。因此，隐含的一年后的一年期即期收益率，$f_{1,2}$ = 8.01%，如果未来一年期即期收益率达到这个水平，将使投资者持有的两个零息债券拥有相同的回报。

It is worth reiterating that the forwards imply distinct yield changes for actual bonds and for constant-maturity rates. The forwards tell how much the yield of a given security —— a longer-term bond —— needs to change to offset an initial yield spread over the short-term rate. Alternatively, the forwards tell how much a given point on the spot curve has to shift to equate holding-period returns across bonds. In the example above, the two-year zero’s yield had to rise by 1.01% and the constant-maturity one-year spot rate had to rise by 2.01%. The 1% difference is due to the so-called “rolling down the yield curve” effect, which we discuss shortly. However, first, we provide a rule-of-thumb relation between initial yield spreads and break-even yield changes —— and some economic intuition about this relation. We compute the implied two-year spot rate one year forward ($f_{1,3}$) by equating the holding-period returns of the three-year zero and the one-year zero over the next year. (Recall that the value of the two-year spot rate after one year determines the holding-period return of what is today a three-year zero.) The left-hand side of Equation (5) is the approximate holding-period return of the three-year zero⁴ (given a selling rate $f_{1,3}$), and the right-hand side is the holding-period return of the one-year zero.

值得重申的是，对于不同债券和不同期限，远期收益率隐含着不同的收益率变化。远期收益率告诉我们，一个给定债券（一个长期债券）的收益率需要改变多少，以抵消相对于短期收益率的初始利差。或者，远期收益率确定即期收益率曲线必须移动多少以使不同债券的持有期回报相等。在上面的例子中，两年期零息债券收益率必须上升1.01％，一年期即期收益率必须上升2.01％。1％的差异是由于所谓的“收益率曲线下滑效应”，我们将稍后讨论。我们提供了初始利差和盈亏平衡收益率变化之间的经验关系，以及关于这种关系的一些经济直觉。我们通过让三年期零息债券的持有期回报与一年期零息债券在下一年的回报相等来计算隐含的一年后的两年期即期收益率（$f_{1,3}$）。（回想以下，一年后两年期即期收益率的值确定了当前三年期零息债券的持有期回报）。等式（5）的左边是近似三年期零息债券的持有期回报（给定卖出收益率$f_{1,3}$），右侧是一年期零息债券的持有期回报。

\[s_3 - Dur_2 * (f_{1,3} - s_3) \approx s_1 . \tag{5}\]

Note that $f_{1,3} - s_3$ is not the three-year zero’s actual subsequent yield change but the break-even yield change implied by the forward rates today. Rearranging Equation (5) gives a rule-of-thumb that the break-even yield change for the three-year zero equals the yield spread divided by the bond’s duration (at horizon): $f_{1,3} - s_3 \approx (s_3-s_1) / Dur_2$. The following observation may be helpful. A large yield spread means that a purchase of a three-year zero financed by the sale of a one-year zero has a large positive “carry.” The profit of this position is the sum of the yield carry ($s_3 - s_1$) and the capital gains or losses caused by the longer zero’s yield changes. The position is bullish —— it profits from falling rates and suffers from rising rates —— but the positive carry provides a cushion against rising rates. The trade will lose money only if the two-year spot rate rises above $f_{1,3}$ in one year.

注意，$f_{1,3} - s_3$不是三年期零息债券随后实际的收益率变化，而是当前远期收益率隐含的盈亏平衡收益率变化。重新排列等式（5）给出了经验法则，三年期零息债券的盈亏平衡收益率变化等于利差除以债券的久期：$f_{1,3} - s_3 \approx (s_3-s_1) / Dur_2$。以下观察可能有帮助，利差大意味着做空一年期零息债券，做多三年期零息债券具有大的正Carry。这个头寸的利润是Carry（$s_3 - s_1$）和由长期零息债券收益率变化引起的资本损益的和。这个头寸是看涨的——从收益率下降中获利，从收益率上升中损失——但是正的Carry是对收益率上升的缓冲，只有当两年期即期收益率在一年内上升至高于$f_{1,3}$才会出现损失。

The break-even yield change $f_{1,3}-s_3$ shows how much the three-year zero’s yield can rise before its carry advantage is offset. However, if an upward-sloping yield curve remains unchanged, the zero’s yield will fall as it rolls down the curve (from $s_3$ to $s_2$). The capital gains from this rolldown tendency provide the three-year zero with an additional cushion against rising rates. The yield advantage component and the rolldown component can be added up to answer the question, “How much should the constant-maturity two-year spot rate change in the next year to make the three-year zero and the one-year zero earn the same return?” The answer is the implied, or break-even, change in the two-year spot rate over the next year ($\Delta f_2$ in column D in Figure 1):

盈亏平衡收益率变化$f_{1,3}-s_3$显示三年期零息债券收益率在其利差优势抵消之前可以上升多少。然而，如果向上倾斜的收益率曲线保持不变，则零息债券的收益率将沿着曲线下降（从$s_3$到$s_2$）。这种下降趋势带来的资本回报为三年期零息债券提供了对收益率上升的额外缓冲。收益率优势部分和收益率下降部分合起来可以回答这样的问题：一年后的两年期即期收益率需要变化多少可以使三年期零息债券和一年期零息债券有同样的回报？答案是下一年的两年期即期收益率的隐含的或盈亏平衡的变化（图1中的D列中的$\Delta f_2$）：

\[\Delta f_2 = (f_{1,3} - s_3) + (s_3 - s_2) = f_{1,3} - s_2 . \tag{6}\]

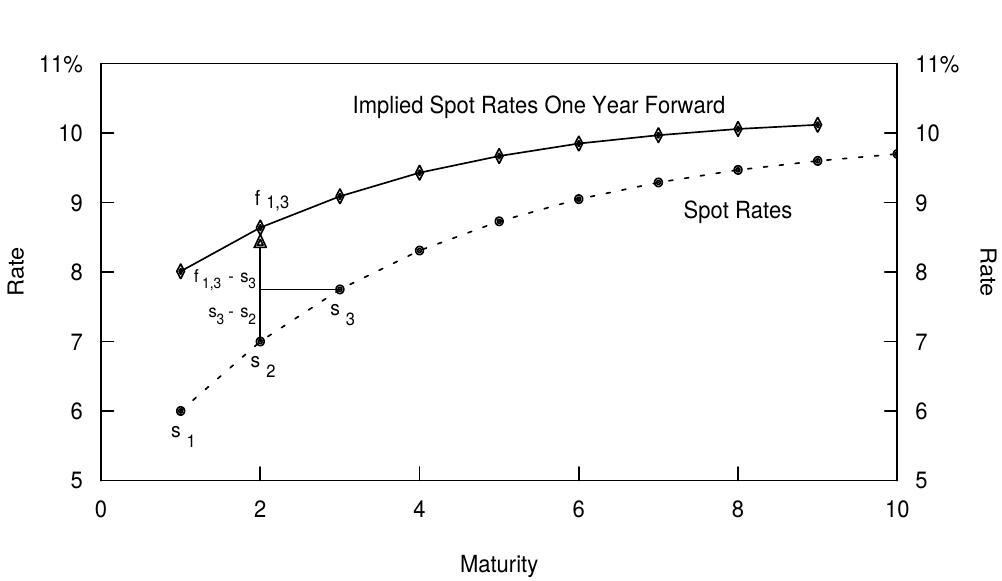
If only the spot rates in Figure 1 are known ($s_1$ = 6%, $s_2$ = 7%, $s_3$ = 7.75%), the yield advantage component is 0.875% ($= (7.75 - 6.00)/2$) and the rolldown component is 0.75% ($= 7.75 - 7.00$). Thus, $\Delta f_2 = 1.625\%$ ($= 0.875 + 0.75$) and $f_{1,3} = 8.625\%$ ($= 7.00 + 1.625$). In words, $\Delta f_2$ is the difference between the implied two-year spot rate one year forward and the two-year spot rate today. Figure 3 illustrates graphically how this break-even yield change is decomposed into the break-even yield change needed to offset the carry ($f_{1,3} - s_3$) and the rolldown yield change ($s_3 - s_2$).⁵

如果仅知道图1中的即期收益率（$s_1$ = 6％，$s_2$ = 7％，$s_3$ = 7.75％），则收益率优势部分为0.875％（$= (7.75 - 6.00)/2$）并且收益率下滑部分为0.75％（$= 7.75 - 7.00$）。因此，$\Delta f_2 = 1.625\%$（$= 0.875 + 0.75$），$f_{1,3} = 8.625\%$（$= 7.00 + 1.625$）。换句话说，$\Delta f_2$是一年后的两年期即期收益率与当前的两年期即期收益率之间的差。图3显示了如何将该收支平衡收益率变化分解为抵消Carry（$f_{1,3} - s_3$）的部分和下滑收益率的部分（$s_3 - s_2$）。

Figure 3. Spot Curve and Implied Spot Curve One Year Forward

An interesting relation exists between the curve of one-year forward rates and the implied spot curve one year forward (columns B and C in Figure 1). The steeper the former curve is, the higher the latter curve must be. A steep curve of one-year forward rates reflects a large rolling yield advantage for long-term bonds over the one-year bond. (We show in the Appendix that the one-year forward rate between maturities n-1 and n is equal to the n-year zero’s rolling yield, that is, its one-year horizon return if the yield curve does not change. Thus, the one-year forward rate $f_{n-1, n}$ is equal to the spot rate $s_n$ plus the rolldown return.) The larger this rolling yield advantage is, the larger the yield increase required to offset it is, and the higher the implied spot curve one year forward is (see the Appendix for details).

在一年期远期收益率曲线和一年后的隐含即期收益率曲线（图1中的B列和C列）之间存在一个有趣的关系。前一个曲线越陡，后一个曲线必须越高。陡峭的一年期远期收益率曲线反映了长期债券相对于一年期债券具有较大的滚动收益率优势。（我们在附录中显示，n-1年和n年之间的一年期远期收益率等于n年期零息债券滚动收益率，也就是在收益率曲线不变的情况下一年期持有期回报。因此，一年期远期收益率$f_{n-1, n}$等于即期收益率$s_n$加上下滑回报。）该滚动收益率优势越大，抵消其所需的收益率增加量越大，并且一年后隐含的即期收益率曲线越高（详见附录）。

Break-Even Yield Changes for Curve-flattening Positions

做平曲线头寸的盈亏平衡收益率变化

We can extend the above analysis to more complex yield curve positions. If the implied spot rates one year forward are realized, all self-financed positions of government bonds will break even (earn a return of 0%). To break even, any position with a positive carry will have to suffer capital losses; the forwards show how large spread changes over the next period would cause capital losses that offset the positive carry. Conversely, any position with a negative carry will have to earn capital gains to break even; thus, forwards imply spread changes that cause such capital gains. The following example clarifies this point.

我们可以将上述分析扩展到更复杂的收益率曲线交易上。如果一年后隐含的即期收益率实现，所有自融资的国债头寸将实现盈亏平衡（赚取0％的回报）。要实现平衡，任何具有正Carry的头寸都必须遭受资本损失；远期收益率显示了下一期（年）利差要变化多少才能使导致的资本损失抵消正的Carry。相反，任何具有负的Carry的头寸都必须获得资本回报才能平衡。因此，远期收益率隐含的利差变化导致资本回报的变化。以下示例说明了这一点。

Consider an investor who has a strong view, with a one-year horizon, that the spot curve will flatten between two- and four-year maturities. He could implement this curve flattening view by selling a three-year zero and by buying with the sale proceeds equal market values of a five-year zero and a one-year zero (which represents cash at horizon).⁶ Such a “barbell-bullet” trade is duration-neutral; thus, the position is not sensitive to parallel changes in interest rates, but it profits from the curve flattening. In a typical yield curve environment, this trade earns a negative carry. That is, when the spot curve is concave (steeper slope in the front end than in the long end), the yield loss of moving from the three-year zero to the one-year zero will be greater than the yield gain of moving from the three-year zero to the five-year zero. For example, in Figure 1 the negative carry is 39 basis points ($0.5 * (6.00 - 7.75) + 0.5 * (8.73 - 7.75) = -0.88 + 0.49 = -0.39$). For the trade to make money, capital gains caused by future flattening of the spot curve must offset the negative carry.

假设一个投资者有强烈的预期，一年之后，两到四年期之间的即期收益率曲线将变平。他可以通过卖出一个三年期零息债券，购买相等市场价值的五年期和一年期零息债券（在期末代表现金）来实施这个曲线变平的预期。这种“杠铃-子弹”交易是久期中性的，因此，该头寸对收益率的平行变化不敏感，但它从曲线变平中获利。在典型形态的收益率曲线情况下，这种交易获得负的Carry。当即期收益率曲线是上凸的（短端比长端更陡），三年期零息债券相对于一年期零息债券的收益率损失将大于三年期零息债券相对于五年期零息债券的收益率增益。例如，在图1中，负Carry是39个基点（$0.5 *（6.00- 7.75）+ 0.5 *（8.73-7.75）= -0.88 + 0.49 = -0.39$）。为了保证交易可以赚钱，由未来变平的即期收益率曲线造成的资本回报必须抵消负的Carry。

The implied spot curve one year forward indicates the future level of the two- to four-year spread at which the trade —— like any bond position with no net investment —— exactly breaks even. This is the sense in which the forward rates “imply” flattening of the spot curve. More curvature in today’s spot curve (a lower one-year rate or five-year rate for a given three-year rate) indicates less attractive terms for a flattening trade (a larger negative carry) and more implied flattening by the forwards (which is needed to offset the negative carry). If today’s spot curve were linear and not at all curved, the flattening trade would give up no yield, and, consequently, the forwards would imply no flattening of the spot curve. The break-even change in the two- to four-year spread would be zero. Finally, if today’s spot curve were convex, the (barbell-bullet) flattening trade would actually pick up yield, and the forwards would imply steepening of the spot curve.

一年后的隐含即期收益率曲线显示了未来的两年期和四年期的利差水平，在该水平上，该交易（如没有净投资的任何债券头寸）完全盈亏平衡。这就是远期收益率“隐含”即期收益率曲线变平的意义。当前的即期收益率曲线的曲率越大（对于给定的三年期收益率，一年期或五年期收益率相对更低），表示做平交易的吸引力越小（较大的负Carry），并且远期收益率隐含的变平程度越大（为了抵消负的Carry）。如果当前的即期收益率曲线是线性的并且完全不弯曲，则做平交易将不产生负的Carry，因此，远期收益率意味着即期收益率曲线将不会变平。两年期至四年期利差的盈亏平衡变化为零。最后，如果当前的即期收益率曲线是下凸的，（杠铃-子弹）做平交易将马上获得正Carry，并且远期收益率将意味着即期收益率曲线变得陡峭。

Note that the break-even change in the (constant-maturity) two- to four-year yield spread depends not only on the barbell’s and the bullet’s initial yields, but also on their rolldown tendencies. When the spot curve is concave, a rolldown return advantage augments the bullet’s yield advantage. (The three-year zero rolls down a steeper part of the curve than the five-year zero, and the one-year zero earns no rolldown return because it has zero duration at horizon.) Thus, the rolling yield curve —— that is, the curve of one-year forward rates —— is even more concave than the spot curve. The amount of implied flattening (which is needed to offset the negative yield carry and the difference in rolldown returns) really depends on the curvature of the rolling yield curve.

注意，两年期到四年期利差的盈亏平衡变化不仅取决于杠铃组合和子弹组合的初始收益率，还取决于其收益率下滑趋势。当即期收益率曲线是上凸的时，下滑回报增加了子弹组合的收益率优势。（相比于五年期零息债券，三年期零息债券（的收益率）在曲线更陡峭的部分发生下滑，而一年期零息债券没有下滑回报，因为它的久期在期末是零）因此，滚动收益率曲线（一年期远期收益率的曲线）比即期收益率曲线更加上凸。隐含的变平程度（用于抵消负的Carry和下滑回报的差异）实际上取决于滚动收益率曲线的曲率。

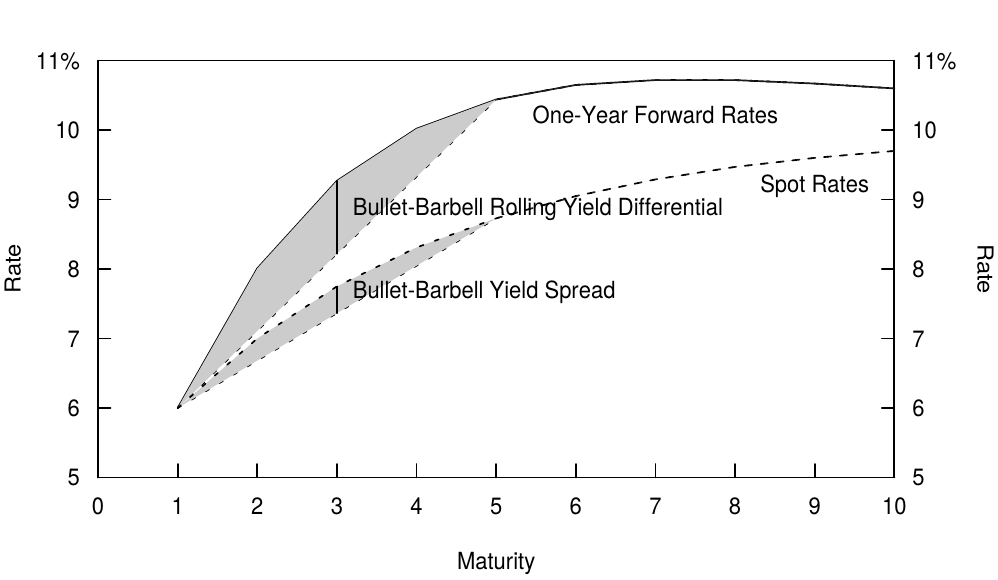
Figure 4 illustrates a typical spot curve and the corresponding curve of one-year forward rates (columns A and B in Figure 1). To evaluate the degree of curvature in these curves, we draw a straight line between a pair of zeros with different maturities (durations). Each point on these lines represents a barbell portfolio of the two zeros. The curvature is measured by the vertical distance between a barbell portfolio and a duration-matched bullet bond. The curvature of the spot curve reflects the bullet-barbell yield spread, while the curvature of the curve of one-year forward rates reflects the bullet-barbell rolling yield differential. The larger the vertical distance between the barbell and the duration-matched bullet is, the more “expensive” the barbell is in the sense that larger curve flattening is needed for the trade to break even. For example, the initial rolling yield differential of 105 basis points at the three-year point ($0.5 * 6.00 + 0.5 * 10.44 - 9.27 = -1.05$) will only be offset if the two- to four-year spread narrows by 52 basis points in one year. The break-even spread change can be computed from column D in Figure 1: $112 - 164 = -52$ basis points.

图4显示出了典型的即期收益率曲线和对应的一年期远期收益率曲线（图1中的A列和B列）。为了计算这些曲线中的曲率，我们在具有不同期限（久期）的一对零息债券之间画一条直线。这些线上的每个点表示一种两个零息债券的杠铃组合。曲率通过杠铃组合与久期匹配的子弹组合之间的垂直距离来测量。即期收益率曲线的曲率反映子弹-杠铃组合的利差，而一年期远期收益率曲线的曲率反映子弹-杠铃组合的滚动收益率差异。杠铃组合与久期匹配子弹组合之间的垂直距离越大，表示杠铃组合越是“昂贵”，因为这意味着要使曲线变平的程度更大才能使交易实现盈亏平衡。例如，三年期的初始滚动收益率差异为105个基点（$0.5 * 6.00 + 0.5 * 10.44 - 9.27 = -1.05$），只有当两年期与四年期的利差在一年里缩小52个基点才会被抵消。盈亏平衡利差变化可以从图1中的D列计算：$112-164 = -52$个基点。

Figure 4. Measuring the Degree of Curvature

THE EXPECTATIONS HYPOTHESIS AND THE YIELD CURVE

预期假说与收益率曲线

How Do Rate Expectations Influence Today’s Yield Curve Shape?

收益率预期如何影响当下的收益率曲线形状？

It is widely agreed that the market’s rate expectations have a strong influence on the yield curve shape. It is much more controversial to argue that such expectations are the only determinant of the yield curve shape.⁷ However, this is roughly what the pure expectations hypothesis (PEH) claims. This hypothesis assumes that all government bonds, regardless of their maturity, have the same near-term expected return. The motivation is that the market prices of bonds are set by risk-neutral traders, whose activity eliminates any expected return differentials across bonds.

众所周知，市场的收益率预期对收益率曲线形状有很大的影响。然而有争议的是，这种预期是收益率曲线形状的唯一决定因素。完全预期假说（PEH）恰恰这样认为。这个假说假设所有政府债券，无论其期限，具有相同的近期预期回报。假说提出的动机是，债券的市场价格是由风险中性交易者设定的，其交易活动消除了不同债券之间的预期回报差异。

If all government bonds have the same near-term expected return, any yield differences across bonds must imply expectations of future rate changes (so that expected capital gains or losses offset the impact of initial yield differences). For example, if investors expect rates to rise and long-term bonds to lose value, they require higher initial yields for long-term bonds than for short-term bonds, making today’s yield curve upward sloping. This kind of break-even argument is similar to the one used in the previous section, except that now the expected (as opposed to realized) returns are being equalized across bonds.

如果所有政府债券都具有相同的近期预期回报，不同债券之间的任何收益率差异都意味着对未来收益率变动的预期（因此预期资本损益抵消了初始收益率差异的影响）。例如，如果投资者预期收益率上升，长期债券价值下降，长期债券的初始收益率要高于短期债券，从而使得当下的收益率曲线向上倾斜。这种盈亏平衡的论证与上一节所使用的类似，除了现在预期（而不是实现的）回报需要在不同债券之间保持相等。

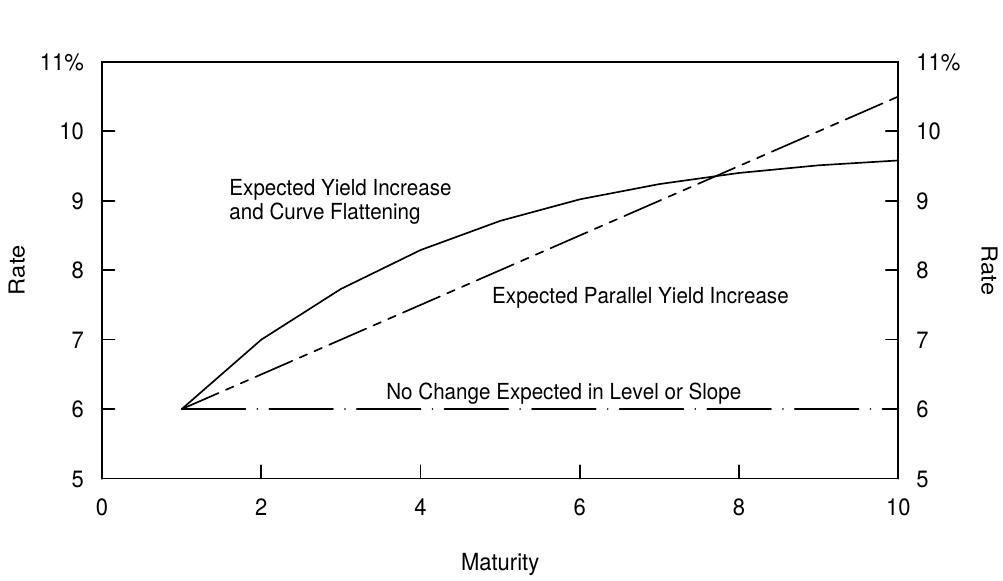
Figure 5 illustrates how different types of expectations influence today’s spot curve (if there are no expected return differences across bonds and if the convexity bias is ignored). Expectations of unchanged future rates lead to a horizontal spot curve, rising rate expectations (for example, a parallel shift of 100 basis points over one year) lead to a linearly upward-sloping spot curve and curve-flattening expectations lead to a concave curve shape. A break-even type of argument can motivate each situation:

图5说明了不同类型的预期如何影响当前的即期收益率曲线（如果债券之间的预期回报没有差异，并且忽略凸度偏差）。未来收益率保持不变的预期导致了水平的即期收益率曲线，预期收益率上升（例如，每年增长100个基点）导致线性向上倾斜的即期收益率曲线，预期曲线变平导致上凸的曲线形状 。一个盈亏平衡式的论证可以解释下面每一种情况：

Figure 5. Spot Curves Given the Market’s Various Rate Expectation

• If the market expects no rate changes, today’s spot curve is flat because no expected gains or losses need to be offset by an initial yield spread.

• 如果市场预期收益率没有变化，当前的即期收益率曲线将是平坦的，因为没有预期盈亏需要被初始利差所抵消。

• If the market expects rates to rise in a parallel fashion, longer-term bonds are expected to earn greater capital losses than shorter-term bonds. An initial yield advantage must offset these expected losses. Because the expected capital losses are proportional to duration, the yield advantage is also proportional to duration. Therefore, today’s spot curve is linearly upward sloping. In a similar way, expectations of declining future rates make today’s spot curve inverted.

• 如果市场预期收益率同时上涨，长期债券预计将比短期债券遭受更大的损失。初始收益率优势必须抵消这些预期损失。由于预期损失与久期成正比，收益率优势也与久期成正比。因此，当前的即期收益率曲线呈线性向上倾斜。以类似的方式，对未来收益率下降的预期使当前的即期收益率曲线倒挂。

• If the market expects the curve to flatten in the future, barbells and other curve-flattening positions are expected to earn capital gains. An initial negative carry must offset these expected capital gains. Therefore, today’s spot curve is concave, and barbell portfolios have lower yields and rolling yields than duration-matched bullet bonds. In a similar way, expectations of future curve steepening tend to make today’s spot curve convex, and barbells have higher yields than bullets.

• 如果市场预期未来的曲线将会变平，杠铃组合和其他做平曲线的头寸预计将获得回报。最初负的Carry必须抵消这些预期的回报。因此，当前的即期收益率曲线是上凸的，杠铃组合的收益率和滚动收益率比久期匹配的子弹组合更低。以类似的方式，对未来曲线变陡峭的期望往往使当前的即期收益率曲线下凸，而且杠铃组合的收益率高于子弹组合。

Expectations versus Risk Premia

预期与风险溢价

We emphasize that the PEH is nothing more than a hypothesis. Much empirical evidence shows that the extreme assumption of equal expected returns across bonds is false. Thus, it is unreasonable to assume that an upward-sloping yield curve reflects only expectations of rising rates. It is at least as reasonable to assume that such a shape reflects only the premium that investors require for holding long-term bonds. (We ignore the convexity bias until the next subsection.) In this light, the numbers in Figure 1 ($s_1$ = 6%, $s_2$ = 7%, $f_{1,2}$ = 8.01%) can be interpreted in two ways.

我们必须强调PEH只不过是假说。许多经验证据表明，假设债券之间相等的预期回报是错误的。因此，假设向上倾斜的收益率曲线仅反映对收益率上升的预期是不合理的。至少可以认为这样的形状只反映投资者持有长期债券所要求的溢价。（我们忽略下一单元提到的凸度偏差）。在这一点上，图1中的数字（$s_1$ = 6%, $s_2$ = 7%, $f_{1,2}$ = 8.01%）可以用两种方式来解释。

• According to the PEH, the one- and two-year zeros have the same expected return over the next year. The return of the shorter zero is known to be 6%. The one-year return of the longer zero will be 6% only if its yield rises to 8.01% (thereby causing capital losses that offset its initial yield advantage). Thus, $f_{1,2}$ reflects the expected level of the one-year spot rate one year hence.

• 根据PEH，一年期和二年期零息债券在次年的预期回报相同。期限较短的零息债券的收益率已知为6％。只有其收益率上升至8.01％（从而导致资本损失抵消其初始收益率优势），则期限较长的零息债券在次年的收益率才为6％。因此，$f_{1,2}$反映了一年后一年期即期收益率的预期水平。

• According to the risk premium hypothesis, $f_{1,2}$ reflects only the longer zero’s one-year expected return and no expected rate changes. Recall that one-year forward rates measure the zeros’ one-year expected returns given no change in the yield curve. If the spot curve is unchanged in a year, the longer zero earns the initial 7% yield plus a 1.01% rolldown return when its yield declines to 6%.

• 根据风险溢价假说，$f_{1,2}$只反映期限较长的零息债券一年后的预期回报，而非预期收益率变动。回想一下，在假定收益率曲线没有变化的前提下，一年期远期收益率衡量零息债券一年后的预期收益率。如果即期收益率曲线在一年内保持不变，则当零息债券的收益率下降至6％时，期限较长的零息债券获得最初的7％收益率加上1.01％的下滑回报。

In both cases, the longer zero will earn the same return over a two-year period (14.49%); this return is known from its 7% annual yield today. However, in the first case the zero is expected to earn 6% in year one and 8.01% in year two, while in the second case, it is expected to earn 8.01% in year one and 6% in year two.

在这两种情况下，期限较长的零息债券将在两年期间获得同样的回报（14.49％），这个回报从当前7％的年化收益率得出。然而，在第一种情况下，零息债券在第一年将获得6％的收益率，在第二年获得8.01％的收益率；而在第二种情况下，零息债券在第一年将获得8.01％的收益率，在第二年获得6％的收益率。

Let us put this example in a broader context. We show in the Appendix (Equation (13)) that, as a linear approximation, the yield change implied by the forwards can be split to an expected change in the n-1 year spot rate over the next year, $E(\Delta s_{n-1})$, and a bond risk premium (that is, the expected return of an n-year bond over the next year in excess of the riskless one-year rate, $BRP_n$):

让我们把这个例子放在更广泛的范围内。我们在附录（等式（13））中显示，作为线性近似，远期收益率所隐含的收益率变化可以分解为下一年的n-1年即期收益率的预期变化，$E(\Delta s_{n-1})$，和债券风险溢价（即，未来一年n年期债券的预期回报超过一年期无风险收益率的部分，$BRP_n$）：

\[f_{1,n} - s_{n-1} \approx E(\Delta s_{n-1}) + BRP_n / (n-1) \tag{7}\]

Equation (7) helps in contrasting different assumptions about the yield curve behavior. For better understanding, one can think of $f_{1,n} - s_{n-1}$ loosely as one measure of the yield curve steepness. Thus, the equation says that the curve steepness reflects market’s future rate expectations, or expected return differentials across bonds, or some combination. The two cases above make two polar assumptions:

等式（7）有助于对比关于收益率曲线行为的不同假设。为了更好的理解，人们可以将$f_{1,n} - s_{n-1}$粗略地看作是收益率曲线陡峭程度的度量。因此，等式表明，曲线陡峭程度反映了市场的未来收益率预期，或不同债券之间的预期回报差异，或某种组合。上述两种情况做出两个极端假设：

• The PEH assumes that $BRP = 0$. Thus, all government bonds have the same near-term expected return as the riskless asset, and forwards reflect only the market’s expectations of future rate changes.

• PEH假设$BRP = 0$。因此，做为无风险资产，所有政府债券具有相同的近期预期回报，而远期收益率仅反映市场对未来收益率变动的预期。

• The risk premium hypothesis assumes that $E(\Delta s_{n-1}) = 0$. Thus, forwards reflect only the near-term expected return differentials across bonds.

• 风险溢价假说假设$E(\Delta s_{n-1}) = 0$。因此，远期收益率仅反映不同债券之间的近期预期回报之间的差异。

In reality, of course, neither polar assumption is correct; the truth lies somewhere between.⁸ Fortunately, the interpretation of forward rates as break-even rates is valid whether forward rates reflect the market’s expectations of future rates, risk premia, or both. We will present some empirical evidence later that indicates that if one of the two polar assumptions has to be chosen, the risk premium hypothesis is the more realistic one.

当然，实际上，两种极端假设都不是正确的，真相介于两者之间。幸运的是，将远期收益率作为盈亏平衡收益率的解释是合理的，无论远期收益率是否反映了市场对未来收益率的预期，或是风险溢价，或是两者都有。我们将在以后提出一些经验证据，如果有必要从两个极端假设中选择一个，风险溢价假说通常更接近现实。

Alternative Versions of the Expectations Hypothesis and the Convexity Bias

预期假说的替代版本和凸度偏差

The bond risk premium is not the only reason that the forward rates are not equal to expected spot rates. Another reason is the so-called convexity bias. The PEH is often identified with two statements: “All bonds have the same near-term expected return” and “forward rates are optimal (unbiased) forecasts of future spot rates.” It turns out that these two statements are not exactly consistent with each other. That is, two distinct versions of the PEH exist; the local expectations hypothesis is associated with the first statement and the unbiased expectations hypothesis is associated with the second statement. The difference between these hypotheses is related to convexity, that is, the nonlinearity in a bond’s price-yield curve.

债券风险溢价不是远期收益率不等于预期即期收益率的唯一原因。另一个原因是所谓的凸度偏差。PEH通常由两种表述定义：所有债券具有相同的近期预期回报；远期收益率是未来即期收益率的最佳（无偏）预测。事实证明，这两句话是不完全相互一致的。也就是说，存在两种不同版本的PEH；局部预期假说与第一个表述相关联，而无偏预期假说与第二个表述相关联。这些假说之间的差异与凸度有关，即债券价格与收益率曲线关系中的非线性部分。

We only try to give here some intuition about the convexity bias. Consider a situation in which the spot curve and the implied forward curves are flat at the 6% level. Because there are no yield differences across bonds and no rolldown, will the expected returns be equal across bonds? No, they will not, because some bonds are more convex than others. Positive convexity can only increase expected return for a given yield; thus, the longer-duration bonds, which exhibit greater convexity, will have higher expected returns. Therefore, even though forward rates equal expected spot rates in this example, all bonds will not have the same expected return. We refer to the impact of convexity on the yield curve shape as the convexity bias.⁹

我们只尝试给出一些关于凸度偏差的直观理解。考虑即期收益率曲线和隐含的远期收益率曲线在6％水平上并且平坦的情况。因为债券之间没有收益率差异，没有下滑回报产生，那么债券的预期回报是否会相等？不会，因为一些债券比其他债券凸度大。正凸度只能提高给定收益率的预期回报，因此，有更大凸度的长久期债券将具有较高的预期回报。因此，即使本例中远期收益率与即期收益率相同，所有债券的预期回报也不会相同。我们将凸度对收益率曲线形状的影响称为凸度偏差。

To conclude, in this section we have described how the market’s rate expectations influence the shape of the yield curve, but we also emphasized that expectations are not the only determinants of the curve. The statement “forward rates show the market’s expectations of future spot rates” is valid only if the bond risk premia and the convexity bias can be ignored. Ordinarily they cannot. In general, it is difficult to say whether the yield curve’s upward slope reflects rising rate expectations or positive bond risk premia. It is equally difficult to say how much of the curvature in the yield curve reflects the market’s flattening expectations and how much of it reflects the convexity bias. We will discuss these issues in the next section.

总而言之，在本节中，我们描述了市场的收益率预期如何影响收益率曲线的形状，但是我们也强调预期不是曲线的唯一决定因素。“远期收益率显示了市场对未来即期收益率的期望”这一说法仅在债券风险溢价和凸度偏差可以忽略的情况下才有效，但是通常这两个因素不能忽略。一般来说，很难说收益率曲线的斜率是否反映了收益率上升的预期或正的债券风险溢价。同样难以说明收益率曲线的曲率反映了多少市场变平的预期，以及反映了多少的凸度偏差。我们将在下一节讨论这些问题。

EMPIRICAL EVIDENCE ABOUT RATE EXPECTATIONS AND FORWARD RATES

收益率预期与远期收益率间的实证结果

Do forwards reflect the market’s rate expectations, required risk premia or both? Are forward rates or current spot rates better forecasts of future spot rates? Are expected bond returns equal across maturities, as the PEH asserts? In this final section, we address these questions and evaluate empirically what we really know about forward rates and the market’s expectations. (We ignore nonlinear effects such as convexity bias and, thus, make no distinction between the different versions of the PEH.)

远期收益率是否反映了市场对收益率的预期，相应的风险溢价，抑或两者兼有？远期收益率与即期收益率，哪个能更好地预测未来即期收益率？是否真如PEH所言，不同期限债券的预期回报相等？在最后一节中，我们解决这些问题，并根据实际情况评估我们对远期收益率和市场预期的理解。（我们忽略诸如凸度偏差的非线性效应，因此不区分PEH的不同版本。）

Because expectations are not observable, academic researchers have studied these questions using two different methods. Many authors examine the forward rates’ ability to predict actual subsequent rate changes and required bond risk premia. Others take a more direct approach and use surveys of interest rate forecasts to proxy for the market’s rate expectations.

由于预期不可观察，学术研究人员使用两种不同的方法研究这些问题。许多作者研究过远期收益率对于实际后续收益率变动和相应债券风险溢价的预测能力。其他人采取更直接的方法，并利用收益率预测调查来代替市场的收益率预期。

Forwards’ Ability to Forecast Future Rate Changes and Risk Premia

远期收益率对于未来收益率变动和风险溢价的预测能力

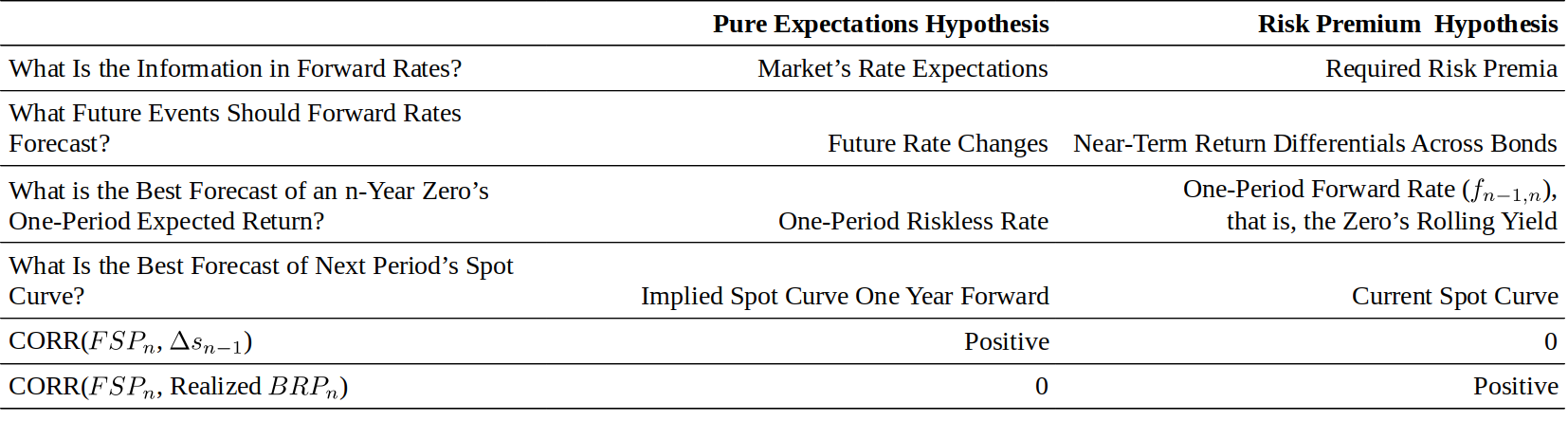
We first examine forwards’ ability to forecast future spot rate changes and realized future bond risk premia. The underlying idea is that the market’s expectations are rational, and any forecast errors are “noise” that should wash out during the sample period. If the PEH holds, forwards are optimal predictors of future spot rates. (By “optimality,” we mean here unbiasedness. The forwards do not need to be very accurate predictors, but they should not contain systematic forecast biases.) However, if the risk premium hypothesis holds, forwards are optimal predictors of near-term expected bond returns, and the current spot curve is the optimal forecast for future spot curves. The implications of the two extreme hypotheses are summarized in Figure 6.

我们首先考察远期收益率对于未来即期收益率变动和未来实现债券风险溢价的预测能力。基本思想是，市场的预期是理性的，任何预测误差都是在抽样期应该清除的“噪音”。如果坚持PEH，那么远期收益率是未来即期收益率的最优预测。（这里的“最优”指的是无偏，远期收益率不需要是非常准确的预测，但不应包含系统性的预测偏差。）然而，如果风险溢价假说成立，远期收益率是债券近期预期回报的最佳预测，当前的即期收益率曲线是未来即期收益率曲线的最佳预测。两个极端假说的含义总结在图6中。

Figure 6. The Implication of Two Hypotheses About the Yield Curve Behavior

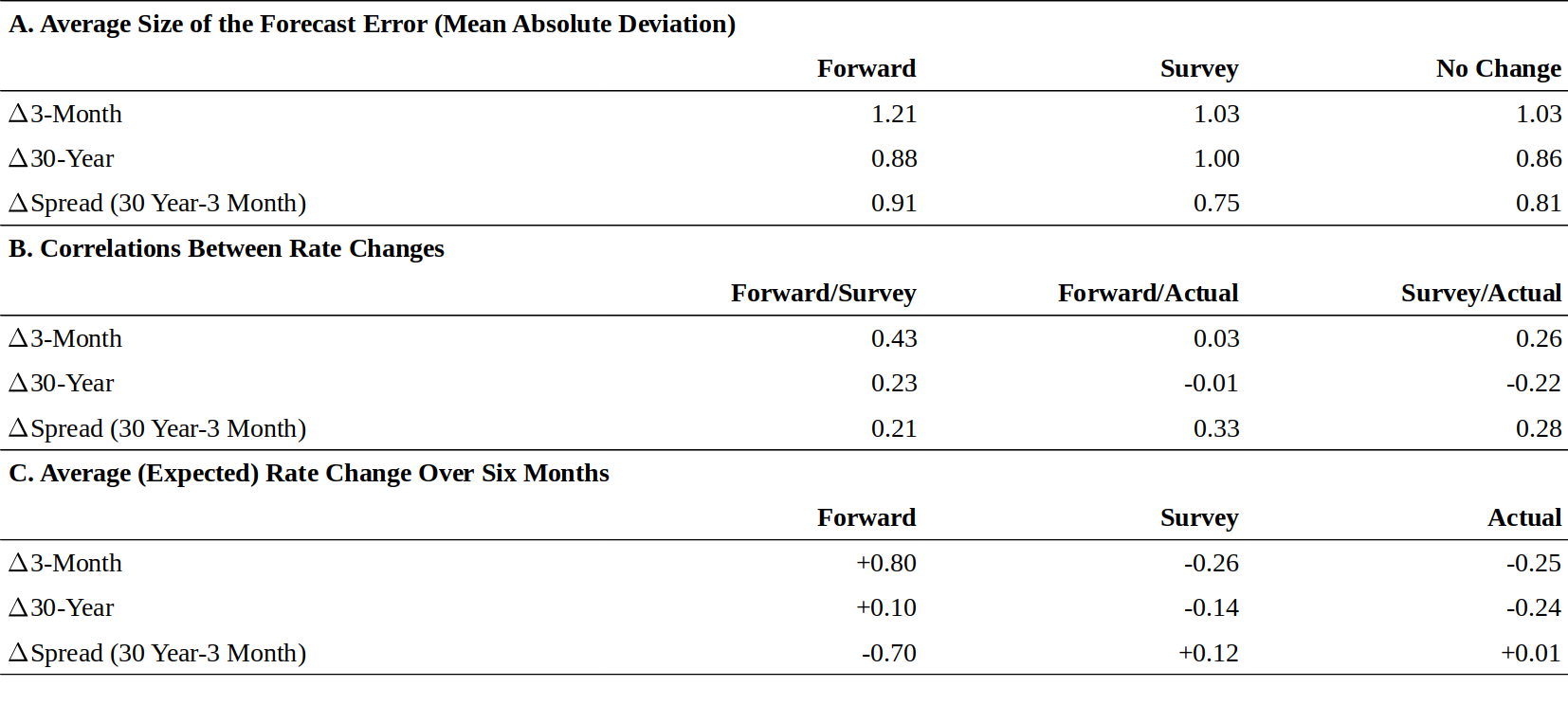
Figure 7 reports the correlation of the forward-spot premium ($f_{n-1,n} - s_1$ or $FSP_n$; see Equation (16) in the Appendix), first, with the subsequent change in the n-1 year spot rate $\Delta s_{n-1}$ over the next month and, second, with the subsequent realized bond risk premium (realized $BRP_n$ or the monthly holding-period return of an n-year zero in excess of the one-month rate). For better understanding, one can view $FSP_n$ as another measure of the yield curve steepness. We compute these correlations for six maturities (three- and six-month bills and estimated two-, three-, four-, and five-year zeros) using monthly Treasury market data from the 1970-94 period.

图7反映了远期-即期溢价（$f_{n-1,n}-s_1$或$FSP_n$，参见附录中的等式（16））的相关性，首先是n-1年即期收益率下一个月的变化$\Delta s_{n-1}$，第二，实现的债券风险溢价（实现的$BRP_n$或n年期零息债券的月度持有收益率超过一月期收益率的部分）。为了更好地理解，可以将$FSP_n$视为收益率曲线陡峭程度的另一个度量。我们使用1970-1994年期间的月度国债市场数据，计算六个不同期限（三月、六月期国库券，和二、三、四和五年期零息债券）上的这些相关性。

Figure 7. Evaluating Forward Rates’ Ability to Predict Monthly Rate Changes and Risk Premia

The first row in Figure 7 provides the main finding. The forward-spot premia are negatively correlated with future changes in long-term rates. That is, when the yield curve is upward sloping, long-term rates do not tend to increase, as the PEH says they should, to offset their initial yield advantage over short-term bonds. Instead, long-term rates tend to decline, causing capital gains that augment the long-term bonds’ yield advantage.¹⁰ Thus, it is not surprising that the forward-spot premia are positively correlated with future bond risk premia (the second row). In the front end of the curve, forwards tend to at least predict the rate direction correctly. Therefore, the optimal forecast of a future spot rate is a weighted average of the current spot rate and the implied spot rate one period forward. In the long end, forwards appear to be inverse indicators of future rate changes. Overall, Figure 7 suggests that the yield curve steepness tends to reflect more near-term expected return differentials across bonds than the market’s rate expectations. These findings are clearly inconsistent with the pure expectations hypothesis, but they may be explained by time-varying bond risk premia.

图7中的第一行显示了主要的发现。远期-即期溢价与长期收益率的未来变化呈负相关。也就是说，当收益率曲线向上倾斜时，长期收益率不会依PEH所说，用收益率增加抵消相对于短期债券的初始收益率优势。相反，长期收益率往往会下降，导致资本回报增加了长期债券的收益率优势。因此，远期-即期溢价与未来债券风险溢价（第二行）正相关并不奇怪。在曲线的前端，远期收益率至少倾向于正确地预测即期收益率变动方向。因此，未来即期收益率的最佳预测是当前即期收益率和隐含即期收益率的加权平均值。长期来看，远期收益率似乎是未来收益率变动的反向指标。总体而言，图7表明，收益率曲线陡峭程度倾向于更多反映债券之间的近期预期回报差异，而不是市场预期。这些发现显然与完全预期假说不一致，但可能由时变的债券风险溢价来解释。

We can relate our empirical analysis to the so-called persistence factors (PFs) that reflect the expectation that spot rates will remain at their current levels.¹¹ The two polar assumptions that we presented earlier —— the PEH and the risk premium hypothesis —— are associated with PFs 0 and 1. A zero value means that today’s spot curve is expected to give way to the implied spot curve one period forward. A unit value means that today’s spot curve is expected to remain unchanged (that is, to persist). Thus, if PF equals zero, forwards are optimal (unbiased) forecasts of future spot rates, and if PF equals one, current spot rates are the optimal forecasts. The PF can be estimated empirically by the slope coefficient in a regression of the annualized realized bond risk premium on the forward-spot premium (see Equation (16) in the Appendix). The value of the PF tells by how much an asset’s near-term expected return increases for a given increase in the forward-spot premium. We find that for maturities beyond one year, for which forwards tend to give the wrong signal about future rate changes, the estimated PFs are greater than one (1.4 - 2.3). For maturities less than one year, for which forwards at least predict the rate direction correctly, the estimated PFs are smaller than one (about 0.8). These findings are consistent with the signs of the correlations in Figure 7.

我们可以将我们的实证分析与所谓持续性因素（PFs，反映即期收益率将保持在目前水平的预期）联系起来。我们前面提到的两个极端假说：PEH和风险溢价假说，与PF有0和1的关系。0意味着当前的即期收益率曲线预期会让位于下一期（年）的隐含即期收益率曲线。1意味着当前的即期收益率曲线预计将保持不变（即持续）。因此，如果PF等于0，则远期收益率是未来即期收益率的最优（无偏）预测；如果PF等于1，则当前即期收益率是最佳预测。PF可以通过实现的年化债券风险溢价关于远期-即期溢价线性回归的斜率系数进行经验估计（见附录中的等式（16））。PF的值指出了在给定的远期-即期溢价增加量时资产的近期预期回报将增加多少。我们发现，对于一年以上的期限，估计的PF大于1（1.4到2.3），远期收益率往往会给出未来即期收益率变化的错误信号。对于不到一年的期限，估计的PF小于1（约0.8），远期收益率至少在预测即期收益率变化方向上是正确的。这些发现与图7中相关性数据的符号一致。

Survey Evidence

来自调查的证据

A more direct approach is to use surveys of bond market analysts’ interest rate forecasts to proxy for the market’s rate expectations. The survey forecasts can be compared with forward rates; any difference should reflect a required risk premium.

更直接的方法是使用债券市场分析师的收益率预测调查来代替市场的收益率预期。预测调查可以与远期收益率进行比较，任何差异都应反映市场对应的风险溢价。

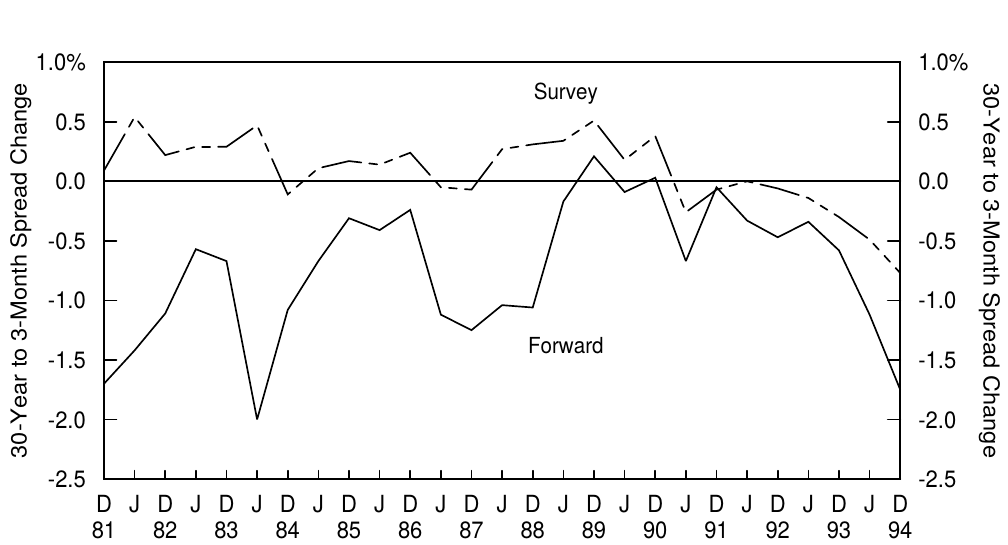
We use the Wall Street Journal’s semiannual survey of Wall Street economists and analysts conducted 27 times between December 1981 and December 1994. In each survey, the participants predict the three-month bill rate and the 30-year bond yield at the end of the next June (December). We compute the expected rate change by subtracting the mid-December (June) rate from the survey median.¹² We then compare these survey forecasts with the yield changes that the forwards imply and with actual subsequent yield changes over each 6.5-month period. The forward yield changes are computed based on the on-the-run Treasury yield curve in mid-December (June). Figure 8 shows the main results separately for the six-month change in the bill rate and the bond rate and their spread.

我们使用《华尔街日报》在1981年12月至1994年12月期间对华尔街经济学家和分析师进行的27次半年度调查。在每次调查中，参与人员预测下个六月（十二月）底的三个月期国库券贴现率和30年期债券收益率。我们通过从调查中位数减去12月（6月）中旬的收益率来计算预期收益率变化。然后，我们将这些调查预测与远期收益率隐含的收益率变化和每隔6.5个月的实际收益率变动进行比较。远期收益率变动由12月（6月）中旬的国债收益率曲线计算。图8分别显示了贴现率和债券收益率及其利差六个月间变动的主要结果。

Figure 8. Accuracy and Bias of Implied Rate Predictions from Forwards and from a Wall Street Journal Survey

Panel A examines the accuracy of the forwards, the surveys and the no-change predictions by showing the average magnitude of the difference between the predicted yield change and the subsequent yield change. (Note that the no-change prediction is consistent with the risk premium hypothesis and that its forecast error is simply the actual yield change.) Panel A shows that all forecasts are quite poor; average errors are of the same order of magnitude as the average yield changes, roughly 100 basis points in six months. Another observation is that the forwards have somewhat larger forecast errors than the no-change predictions, suggesting that the current spot curve predicts future spot curves better than the implied forward curve does. Given the small number of observations, these differences are not statistically significant. A more serious problem regarding the forwards’ predictive ability is that long-term rates tend to move away from the forwards, not toward them —— recall the evidence in Figure 7. However, the negative correlation is quite small in this sample (-0.01), and the expert forecasters have been even worse predictors of long-rate changes (the correlation is -0.22 in panel B). Panel C is the most interesting part of Figure 8. It reveals a systematic bias in the forward rates; during the 13-year period, the forwards typically implied rising short-term and long-term rates and a flattening yield curve, unlike the survey forecasts and the actual rate changes.

表A通过显示预测收益率变化与后续收益率变化之间差异的平均来检查远期收益率预测、调查预测和无变化预测的准确性。（注意，无变化预测与风险溢价假说一致，其预测误差为实际收益率变化。）表A显示，所有预测都相当差；平均误差与平均收益率变化的数量及相同，在六个月内大致为100个基点。另一个观察结果是，远期收益率预测误差比无变化预测有更大的预测误差，这表明当前的即期收益率曲线比隐含的远期收益率曲线能更好地预测未来的即期收益率曲线。鉴于观察数量少，这些差异不具有统计学意义。回顾图7中的证据，远期收益率预测能力的一个更严重的问题是，长期收益率往往偏离远期收益率而不是向其靠拢。但是，在本样本中的负相关性相当小（-0.01），专家对长期变化的预测更为糟糕（表B中相关系数为-0.22）。表C是图8中最有趣的部分。它揭示了远期收益率的系统性偏差；在13年期间，远期收益率通常意味着短期和长期收益率上升，收益率曲线变平，这与调查预测和实际收益率变化不同。

Why are the forwards’ implied rate predictions higher than survey forecasts and actual rate changes? A possible explanation is that the market requires a positive risk premium for holding the long-term bond. In fact, we can use the survey forecasts of future rates to compute a direct estimate of the average bond risk premium. The difference between the yield change implied by the forwards and the expected future yield change is approximately proportional to the risk premium. The 106 (80 - (-26))-basis point difference for the three-month bill translates to an average annualized risk premium of 53 basis points.¹³ A similar calculation shows that the 24 (10 - (-14))-basis point difference for the 30-year bond translates to an average annualized risk premium of 480 basis points. These findings suggest that positive bond risk premia exist.

为什么远期收益率预测的收益率高于调查预测和实际收益率变动？可能的解释是，市场对持有长期债券要求正的风险溢价。事实上，我们可以使用未来收益率的调查预测来计算平均债券风险溢价的直接估计。远期收益率所隐含的收益率变动和预期未来收益率变化之间的差异大致与风险溢价成正比。三月期国库券贴现率106（80-（-26））基点的差异转换为53个基点的平均年化风险溢价。类似的计算显示，30年期债券的24（10-（-14））基点的差异转换为480个基点的平均年化风险溢价。这些发现表明存在正的债券风险溢价。

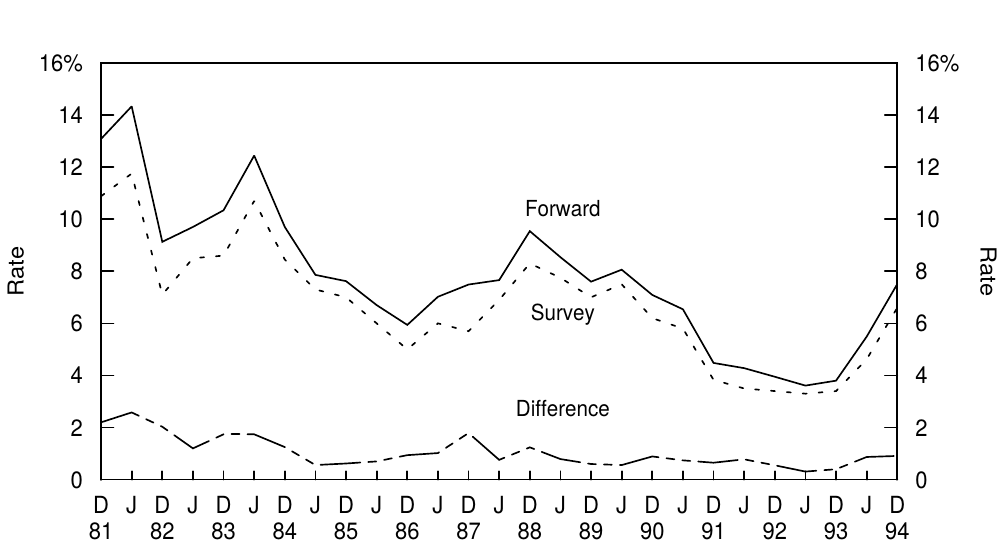
Figure 9 shows how consistently the forward prediction of the three-month rate exceeds the survey forecast. Both series move together with the actual three-month bill rate (which is typically between the two series). As explained above, the difference between the two series is proportional to a bond risk premium. Figure 9 shows that this risk premium is not constant over time. Its time variation appears economically sensible in that the premium is exceptionally high around the 1982 recession and after the 1987 stock market crash when a recession was widely expected. The premium was quite low in 1993, despite the yield curve steepness, and it rose substantially in 1994.¹⁴

图9显示了三月期收益率的远期收益率预测一致超过了调查预测。这两列预测与实际的三月期国库券贴现率（通常在两个系列之间）一起移动。如上所述，两列预测之间的差异与债券风险溢价成正比。图9显示，这种风险溢价不是恒定的。其时变性经济上似乎是合理的，因为1982年经济衰退期以及1987年股市崩溃之后，当经济衰退得到广泛预期时，溢价是非常高的。尽管收益率曲线陡峭，但溢价在1993年相当低，并在1994年大幅上涨。

Figure 9. Forward- and Survey-Expected Three-Month Treasury Bill Rate Six Months Ahead

Figure 10 plots the implied forward changes in the three-month to 30-year yield spread and the corresponding survey forecasts. Forwards have quite consistently implied yield curve flattening, while the survey respondents were, until recently, often predicting curve steepening. We noted earlier that the typical concave yield curve shape causes forwards to imply curve flattening, and we conjectured that most of this implied flattening probably reflects the value of convexity rather than actual flattening expectations. Figure 10 is consistent with this conjecture. The difference between the two series in Figure 10 should, in fact, be a reasonable measure of the market price of convexity.

图10显示了远期收益率隐含的三月期-30年期利差的变化以及相应的调查预测。远期收益率相当一贯地隐含收益率曲线变平，而直到最近，调查结果经常预测曲线变陡。我们早些时候注意到，典型的上凸收益率曲线形状导致远期收益率隐含着曲线变平，我们推测，大多数这种隐含的平坦化可能反映了凸度的价值，而不是实际的预期。图10与这个猜想是一致的。实际上，图10中的两列预测之间的差应该是对凸度市场价值的合理衡量。

Figure 10. Forward- and Survey-Expected Yield Curve Steepening Six Months Ahead

Investment Implications of the Empirical Findings

实证结果在投资中的实践

Overall, the empirical evidence is much more consistent with the risk premium hypothesis than with the pure expectations hypothesis. Forwards tell us more about near-term expected return differentials across bonds than about future rate changes. If either today’s spot curve or the implied spot curve one period forward must be used as a predictor of the next period’s spot curve, the evidence supports the use of the former as the neutral base case. These findings have obvious investment implications; rolling yield differentials between bonds or the corresponding break-even yield changes provide potentially useful relative value indicators for duration-extension trades. Intuitively, because the rate changes that forwards imply are not realized, on average, bonds with high rolling yields tend to keep their yield and roll down advantage. Similarly, break-even changes of yield spreads may be good relative value indicators for duration-neutral yield curve positions such as barbells versus bullets. In later reports, we will evaluate the historical performance of these indicators and traditional cheapness indicators such as yield spreads.

总体而言，经验证据与风险溢价假说更为一致，而不是完全预期假说。远期收益率更多告诉我们不同债券间的近期预期回报差异，而不是未来的收益率变化。如果必须选择当前的即期收益率曲线或隐含的即期收益率曲线作为下一期（年）曲线的预测，实证结果支持使用前者作为中性基准。这些发现具有明显的投资意义；不同债券之间的滚动收益率差异，或相应的盈亏平衡收益率变动为增加久期的交易策略提供了潜在有用的相对价值指标。直观地看，由于远期收益率隐含的收益率变化没有实现，平均而言，滚动收益率较高的债券往往会保持期收益率优势和下滑收益率优势。类似地，利差的盈亏平衡变化可能是久期中性头寸（如杠铃-子弹组合）的良好相对价值指标。在后来的报告中，我们将评估这些指标的历史表现和传统的廉价指标（如利差）。

More generally, the empirical failure of the pure expectations hypothesis is good news for active managers. If all bond positions always had the same near-term expected returns, it would be extremely difficult to add value. Therefore, our findings provide some empirical justification for yield-seeking active investment strategies.

更一般的说，完全预期假说在实证上的失败对于主动管理的经理是个好消息。如果所有债券头寸总是具有相同的近期预期回报，那么增加价值将是非常困难的。因此，我们的研究结果为寻求主动的投资策略提供了一些经验论证。

APPENDIX. RELATIONS BETWEEN FORWARD RATES, EXPECTED RATE CHANGES AND EXPECTED RETURNS

附录：远期收益率、预期收益率变化和预期回报之间的关系

This Appendix shows how forward rates are related to expected spot rate changes and expected holding-period returns and how one-year forward rates are related to implied spot rates one year forward. These relations are linear approximations that ignore nonlinear effects such as the convexity bias. Equation (3) shows how the annualized forward rate between maturities m and n is related to m- and n-year spot rates. By taking a first-order approximation of both sides of this equation and rearranging, we get a nice linear relation:

本附录显示了远期收益率如何与预期即期收益率变动和预期持有期回报建立关系，以及一年期远期收益率与一年后的隐含即期收益率如何相关。这些关系是忽略诸如凸度偏差的非线性效应的线性近似。等式（3）显示了期限m年和n年之间的年化远期收益率如何与m年和n年期即期收益率有关。通过对该等式的两边进行一阶近似并重新排列，得到一个很好的线性关系：

\[f_{m,n} \approx \frac{ns_n - ms_m}{n-m}. \tag{8}\]

To compute the implied spot curve one year forward, we set m = 1:

为了计算一年后的隐含即期收益率，我们设m = 1：

\[f_{1,n} \approx \frac{ns_n - s_1}{n-1}. \tag{9}\]

Equation (10) shows the n-year zero-coupon bond’s holding period return over the next period ($h_n$). The zero earns its initial yield, $s_n$, plus a capital gain which is approximated by the product of the zero’s duration at horizon (n-1) and its yield change.

等式（10）显示了下一期（年）的n年期零息票债券持有期回报（$h_n$）。零息债券获得其初始收益率$s_n$，再加上一个资本增益，其近似值为零息债券的久期（n-1）和其收益率变化的乘积。

\[h_n \approx s_n + (n-1)*(s_n - s^{\ast}_{n-1}) , \tag{10}\]

where $s^{\ast}$ is the next period’s rate (at which the bond is sold). Now we substitute Equation (10) into Equation (9), noting that $ns_n = s_n + (n-1)*s_n$:

其中$s^{\ast}$是下一期（年）的收益率（债券出售期）。现在我们将等式（10）代入式（9），注意到$ns_n = s_n + (n-1)*s_n$：

\[f_{1,n} \approx \frac{h_n + (n-1)*s^{\ast}_{n-1} - s_1}{n-1} = s^{\ast}_{n-1} + \frac{h_n - s_1}{n-1} . \tag{11}\]

We call $h_n - s_1$ (the one-year holding-period return in excess of the short-term rate) the realized risk premium of the n-year zero. Because the equality in Equation (11) holds for realized returns, it also should hold in expectations if they are rational. Thus,

我们称$h_n - s_1$之为n年期零息债券实现的风险溢价（一年持有期回报超过短期收益率的部分）。因为等式（11）中的等式对实现的回报成立，所以如果等式是合理的，也应该对预期同样适用。因此，

\[f_{1,n} \approx E(s^{\ast}_{n-1}) + \frac{BRP_n}{n-1} , \tag{12}\]

where $BRP_n$ (the bond risk premium) is the expected holding-period return of an n-year zero in excess of the riskless one-year rate or $E(h_n - s_1)$. Subtracting $s_{n-1}$ from both sides of Equation (12) gives the break-even change in the n-1 year spot rate:

$BRP_n$（债券风险溢价）是指n年期零息债券的预期持有期回报超过一年期无风险收益率的部分或$E(h_n - s_1)$。从等式（12）的两端减去$s_{n-1}$得出了n-1年期即期收益率的盈亏平衡变化：

\[\Delta f_{n-1} \equiv f_{1,n} - s_{n-1} \approx E(\Delta s_{n-1}) + \frac{BRP_n}{n-1} , \tag{13}\]

where $\Delta s_{n-1} = s_{n-1}^{\ast} - s_{n-1}$. (Note that $\Delta s_{n-1}$ denotes actual rate change over time, whereas $\Delta f_{n-1}$ is the difference between two rates that are known today.) Equation (13) states that the break-even change in the n-1 year spot rate, implied by the forwards, is equal to the sum of the expected change in the n-1 year spot rate over the next year and the bond risk premium of the n-year zero (divided by n-1). The information in the forward rates reflects either expected future yield changes, or expected bond risk premia, or some combination of the two.

其中$\Delta s_{n-1} = s_{n-1}^{\ast} - s_{n-1}$（注意，$\Delta s_{n-1}$表示实际收益率变化，而$\Delta f_{n-1}$是当前已知的两个收益率之间的差）。等式（13）表明，远期收益率隐含的n-1年期即期收益率的盈亏平衡变化等于下一年n-1年期即期收益率预期变化和n年期零息债券风险溢价（除以n-1）的和。远期收益率的信息反映了预期的未来收益率变化或预期的债券风险溢价，或两者的某种组合。

Similarly, we can compute an approximation of the one-year forward rates (m = n-1 in Equation (8)):

类似地，我们可以计算一年期远期收益率的近似值（等式（8）中令m = n-1））：

\[f_{n-1,n} \approx ns_n - (n-1)*s_{n-1} = s_n + (n-1)*(s_n - s_{n-1}). \tag{14}\]

Now we substitute Equation (10) into Equation (14):

现在我们将等式（10）代入式（14）：

\[f_{n-1,n} \approx (n-1)*\Delta s_{n-1} + h_n . \tag{15}\]

If the yield curve remains unchanged, the first term in the right-hand side of Equation (15) equals zero and $f_{n-1,n} = h_n$. In other words, the one-year forward rate is equal to a zero’s holding-period return given an unchanged yield curve, or its rolling yield. Equation (14) shows that such return is equal to a sum of the initial yield and the rolldown return (the zero’s duration at horizon (n-1) multiplied by the amount that the zero rolls down the yield curve as it ages).

如果收益率曲线保持不变，则等式（15）右边的第一项等于零并且$f_{n-1,n} = h_n$。换句话说，给定不变的收益率曲线，一年期远期收益率等于一个零息债券的持有期回报，或其滚动收益率。等式（14）表明，这收益率等于初始收益率与下滑收益率（零息债券在持有期末的久期（n-1）乘以债券随时间在收益率曲线上下滑的量）的和。

We can subtract $s_1$ from both sides of Equation (15) to get the forward-spot premium ($f_{n-1,n} - s_1$ or $FSP_n$) and realized risk premium ($h_n - s_1$), and then take expectations:

我们可以从等式（15）的两边减去$s_1$，以获得远期-即期溢价（$f_{n-1,n} - s_1$或$FSP_n$）和实现的风险溢价（$h_n - s_1$），然后：

\[FSP_n \equiv f_{n-1,n} - s_1 \approx (n-1) * E(\Delta s_{n-1}) + BRP_n . \tag{16}\]

A comparison of Equations (13) and (16) shows that the forward-spot premium is proportional to the break-even yield change:¹⁵ $FSP_n = (n-1) * \Delta f_{n-1}$. Intuitively, $FSP_n$ measures the rolling yield advantage of the n-year zero over the riskless one-year zero, while $\Delta f_{n-1}$ shows how large change in the n-1 year spot rate is needed to offset such a rolling yield advantage. The ratio of proportionality is n-1 because the product of duration-at-horizon and the break-even yield change gives a capital loss that is as large as the rolling yield advantage. Figure 11 illustrates this relation. The top panel shows a spot curve and the corresponding curve of one-year forward rates (rolling yields) which increase linearly with maturity. If the spot curve remains unchanged over the next year, the ten-year zero earns its annual yield 10.50% as well as a rolldown return of 4.50% (nine years end-of-horizon duration times 50 basis points rolldown yield change). Thus, its holding-period return is 15% if the spot curve does not change over the next year —— as shown by the right-most point on the curve of one-year forward rates. The ten-year zero has a 9% rolling yield advantage over the one-year zero. The lower panel shows the implied spot curve one year forward (together with the same spot curve as in the top panel); that is, the break-even levels of future spot rates that would offset the longer-term bonds’ rolling yield advantage over the one-year zero. The nine-year spot rate needs to increase by 100 basis points to cause a 9% capital loss for today’s ten-year zero (whose maturity is nine years after a year). Similar calculations for various-maturity zeros show that a parallel increase of 100 basis points would make all government bonds earn the same 6% holding-period return as the one-year zero. (If convexity effects are taken into account, the break-even yield shift would not be exactly parallel.)

等式（13）和（16）的比较表明，远期-即期溢价与盈亏平衡收益率变化成正比：$FSP_n = (n-1) * \Delta f_{n-1}$。直观上，$FSP_n$衡量了n年期零息债券相比于无风险一年期零息债券的滚动收益率优势，而$\Delta f_{n-1}$则显示出n-1年即期收益率需要变化多少来抵消这种滚动收益率优势。比例为n-1，因为久期和盈亏平衡收益率变化的乘积给出了与滚动收益率优势一样大的资本损失。图11说明了这种关系。上图显示了一个即期收益率曲线和相应的一年期远期收益率（滚动收益率）曲线，随着期限呈线性增长。如果即期收益率曲线在未来一年保持不变，那么十年期零息债券的年化收益率为10.50％，下滑收益率为4.50％（期末九年久期乘以50个基点的收益率下滑变动）。因此，如果即期收益率曲线在下一年没有变化，其持有期回报为15％，如一年期远期收益率曲线上最右点所示。十年期零息债券较一年期零息债券有9%的滚动收益率优势。下图显示了一年后的隐含即期收益率曲线（与上图相同的即期收益率曲线一起）;未来即期收益率的盈亏平衡水平将抵消长期债券较一年期零息债券的滚动收益率优势。九年期即期收益率需要增加100个基点，导致当前十年期零息债券（一年后其期限为九年）的资本损失为9％。各期限零息债券的类似计算表明，平均上涨100个基点将使所有国债的持有期回报与1年期零息债券相同。（如果考虑到凸度效应，盈亏平衡收益率的变化并不完全平行地发生。）

Figure 11. Link Between Zeros’ Rolling Yields and Break-Even Spot Rate Changes

The link between initial rolling yields and the break-even changes in the spot rates is straightforward because the relationship is mathematical. If today’s spot curve and the rolling yield curve were flatter than in the top panel in Figure 11, a smaller increase in the spot curve would be needed to offset the long-term bonds’ rolling yield advantage over the one-year zero, and the forwards would imply smaller rate increases. If today’s spot curve were inverted, long-term bonds would even have lower yields and rolling yields than the one-year zero, and the forwards would imply a rate decline to offset the long-term bonds’ rolling yield disadvantage. If today’s spot curve were upward sloping and concave (the “typical” shape; see Figure 4, which corresponds to the top panel in Figure 11), the forwards would imply rising rates and flattening curve to offset the rolling yield advantage of long-term bonds and steepening positions (bullets versus barbells; see Figure 3, which corresponds to the lower panel in Figure 11).

初始滚动收益率与即期收益率盈亏平衡变化之间的联系直接依赖于数学推导。如果当前的即期收益率曲线和滚动收益率曲线比图11中的曲线更平，则即期收益率曲线需要稍微升高以抵消长期债券相较一年期零息债券的滚动收益率优势，而远期收益率将隐含着较小的收益率增长。如果当前的即期收益率曲线倒挂，长期债券相较一年期零息债券具有更低的收益率和滚动收益率，而远期收益率则隐含着收益率下降以抵消长期债券的滚动收益率劣势。如果当前的曲线是向上倾斜和上凸的（“典型”形状，参见图4，对应于图11中的上半部分），则远期收益率将隐含着收益率上升和曲线变平以抵消长期债券和做陡头寸（子弹-杠铃组合，参见图3，其对应于图11中的下半部分）的滚动收益率优势。

LITERATURE GUIDE

文献指南

Broad Surveys

综述

• Shiller, “The Term Structure of Interest Rates,” Handbook of Monetary Economics, 1990.
• McEnally and Jordan, “The Term Structure of Interest Rates,” Handbook of Fixed Income Securities, 1995.

On the Alternative Versions of the Pure Expectations Hypothesis and the Convexity Bias

关于完全预期假说的替代版本与凸度偏差

• Cox, Ingersoll, and Ross, “A Re-examination of Traditional Hypotheses about the Term Structure of Interest Rates,” Journal of Finance, 1981.
• Campbell, “A Defense of Traditional Hypotheses about Term Structure of Interest Rates,” Journal of Finance, 1986.

On the Forward Rates’ Ability to Predict Future Rate Changes and Future Bond Risk Premia

关于远期收益率预测未来收益率的能力与未来债券风险溢价

• Shiller, Campbell and Schoenholtz , “Forward Rates and Future Policy: Interpreting the Information in the Term Structure of Interest Rates,” Brooking Papers on Economic Activity, 1983.
• Fama, “The Information in the Term Structure” Journal of Financial Economics, 1984.
• Mankiw, “The Term Structure of Interest Rates Revisited,” Brooking Papers on Economic Activity, 1986.
• Fama and Bliss, “The Information in Long-Maturity Forward Rates,” American Economic Review, 1987.
• Hardouvelis, “The Term Structure Spread and Future Changes in Long and Short Rates in the G7 Countries: Is There a Puzzle?,” Journal of Monetary Economics, 1994.
• Campbell, “Some Lessons from the Yield Curve,” National Bureau of Economic Research working paper #5031, 1995.

On Comparing Survey Expectations and the Forward Rates’ Implied Expectations of Future Rates

关于比较调查得到的与远期收益率隐含的预期未来收益率

• Froot, “New Hope for the Expectations Hypothesis of the Term Structure of Interest Rates,” Journal of Finance, 1989.
• Hafer, Hein and MacDonald, “Market and Survey Forecasts of the Three-Month Treasury Bill Rate,” Journal of Business, 1992.
• DeBondt and Bange, “Inflation Forecast Errors and Time Variation in the Term Premia,” Journal of Financial and Quantitative Analysis, 1992.

1. In practice, the spot rates are rarely inferred from the zero-coupon bond (STRIPS) prices because STRIPS differ from the more common Treasury coupon bonds in terms of liquidity and tax treatment. More often, the spot curve is estimated from the prices of all or most Treasury coupon bonds. Once the spot curve is known, it is a matter of algebra to construct the par yield curve which many investors prefer to follow. Alternatively, if the par curve is known, it is easy to construct the spot curve. For details, see Using STRIPS in a Treasury Portfolio. Janet Showers. Salomon Brothers Inc. August 1992. and Overview of Forward Rate Analysis. Salomon Brothers Inc. May 1995. 实际上，零息债券（STRIPS）价格很少用来推断即期收益率，因为在流动性和税收处理方面，STRIPS与更为常见的国债不同。通常，即期收益率曲线是根据所有或绝大多数国债的价格估计的。一旦得到即期收益率曲线，构建投资者倾向于使用的票面收益率曲线就只是一个代数的问题。同样的，如果票面收益率曲线是已知的，则很容易构造即期收益率曲线。详细过程请参考《Using STRIPS in a Treasury Portfolio》（Janet Showers. Salomon Brothers Inc. August 1992）和《Overview of Forward Rate Analysis》（Salomon Brothers Inc. May 1995） ↩︎

2. To simplify notation, this report focuses on spot rates rather than on par yields. Moreover, all analysis is presented using one-year forward rates and annual compounding frequency. In practice, semiannual compounding and three-month forward rates are more popular, but the equations would have to include various annualization terms. 为了简化符号，本报告重点关注即期收益率，而不是票面收益率。此外，所有分析都使用一年期远期收益率和年度付息频率来表示。实际上，半年度付息和三月期远期收益率更受欢迎，但等式必须包括各种不同的年化期限。 ↩︎

3. The forward path is computed by fixing m = n - 1 and letting to vary from 0 to 9. The implied spot curve one year forward is computed by fixing m = 1 and letting n vary from 2 to 10, in a similar way, we can construct the forward path of any constant-maturity rate or the implied spot curve for any future horizon. 通过固定m = n-1并使其从0变化到9来计算远期收益率路径。通过固定m = 1并使n从2变化到10来计算一年后隐含的即期收益率曲线，类似地，我们可以构建任何期限的远期收益率或隐含的即期收益率曲线。 ↩︎

4. The holding-period return of a three-year zero over the next year is equal to its initial yield ($s_3$) plus the capital gains or losses caused by any yield change. In this example, we use linear approximation of the capital gains (percentage price change equals minus duration times yield change), ignoring convexity effects. For this reason, the forward rate $f_{1,3}$ that we compute will be 1.5 basis points lower than that in Figure 1 (which is computed without any approximation error). 下一年三年期零息债券的持有期回报等于其初始收益率（$s_3$）加上任何收益率变动引起的资本损益。在这个例子中，我们使用线性近似的资本回报（百分比价格变化等于负久期乘以收益率变化），忽略凸度影响。因此，我们计算的远期收益率$f_{1,3}$将比图1中的（没有任何近似误差计算）低1.5个基点。 ↩︎

5. The x-axis in Figure 3 (and in subsequent figures) is denoted as maturity, but it could as well be denoted as Macaulay duration because for zeros, duration equals maturity. (This report does not emphasize the distinction between Macaulay duration and modified duration.) 图3（和后续图中）的x轴代表期限，但也可以代表Macaulay久期，因为零息债券的久期等于期限。（本报告不强调Macaulay久期与修改久期的区别） ↩︎

6. It may seem puzzling that a view about two- to four-year spread is implemented by trading three- and five-year zeros. The reason is that, in this example, the investor has a view about the spread change in one year’s time and the zeros’ maturities shorten by one year over the horizon. If the investor had a view with an immediate horizon, he would implement it by selling twos and buying fours and cash. 2-4年期的利差通过交易三年期和五年期零息债券来实现，这看起来很令人困惑。原因在于，在这个例子中，投资者对一年内的利差变动有一个看法，而零息债券的期限在这一年内缩短了一年。如果投资者对当前利差有一个观点，他将通过做空两年期债券并做多四年期债券和持有现金来实施。 ↩︎

7. This report takes the market’s rate expectations as given, except that this footnote briefly discusses the economic determinants of these expectations. An old Wall Street adage —— that the central bank determines the level of short-term rates while the market’s inflation expectations drive the long-term rates —— is an oversimplification, but probably captures the main determinants of rate behavior, (i) Market participants are likely to have clearer expectations regarding the near-term behavior of short rates than about more distant events. These expectations are closely related to the market’s view on the economic conditions and on the direction of monetary policy, if the market expects an increase in economic growth rate and in credit demand, it often expects both the real rates and the inflation to increase, and vice versa. Moreover, central banks often try to influence inflation rates and economic growth by raising short-term (nominal and real) rates when fast economic growth and capacity constraints are risking an inflation pickup and decreasing short rates when the economy is in a recession. The bond market appears to incorporate expectations of such countercyclic monetary policy into the term structure. Thus, the market’s expectations about short-term rate changes may be reasonably flat when the monetary policy is inactive and declining (rising) in periods when the central bank has begun to actively ease (tighten) monetary policy. Central banks often adjust short rates gradually, in trends; thus, the first easing (tightening) moves may create market expectations of further rate declines (increases). However, expectations also may have a mean-reverting component. If the market perceives certain rate levels to be “normal,” it may expect rate changes even if the monetary policy is inactive but short rates are exceptionally high (1981-82) or low (1992-93). (ii) The market’s distant rate expectations probably reflect mainly its long-term inflation views, which are influenced by factors such as the country’s inflation history, the size of the government debt and budget deficits (government’s incentive to “monetize” debt), the strength of anti-inflationary forces (central bank independence, discipline from financial markets, political clout of long-term savers versus debt holders), and the exchange rate policy. The market’s expectations about the real rates in the long run probably move quite slowly, based on its perception of the future investment-saving balance. 本报告假定市场预期已经给定的，本注简要讨论了这些预期的经济决定因素。经典的华尔街格言——央行决定短期收益率的水平，而市场的通胀预期推动长期收益率——是过于简练的，但依然可以捕捉到收益率行为的主要决定因素，（1）相较于更远的事件，市场参与者可能对短期收益率的近期行为有更明确的预期。这些预期与市场对经济状况和货币政策方向的看法密切相关，如果市场预期经济增长率和信贷需求将有所增长，则往往预计实际收益率和通货膨胀率都会上涨，反之亦然。此外，央行经常试图在经济快速增长和生产力制约因素导致通货膨胀率快速上升时通过提高（名义和实际）短期收益率来影响通货膨胀率和经济增长，或者在经济衰退期降低短期收益率。债券市场似乎会将这种反周期货币政策的预期纳入到期限结构中。因此，当央行的货币政策不积极时，市场预期短期收益率变动不大，当央行开始积极放松（收紧）货币政策时，市场预期短期收益率下降（上涨）。中央银行往往顺势逐步调整短期收益率，因此，第一次宽松（紧缩）举措可能会导致市场预期收益率进一步下降（上升）。然而，预期也可能有一个均值回归的成分。如果市场认为存在某个“正常”水平的收益率，当短期收益率异常高（如1981-82）或低（如1992-93）时依然可能预期收益率发生变动，即使这时货币政策不积极。（2）市场的长期收益率预期可能主要反映关于长期通胀的观点，这些观点受到国家通货膨胀历史，政府债务规模和预算赤字（政府鼓励“货币化”债务），抗通货膨胀力量（中央银行独立、金融市场纪律、长期储户对债权人的政治影响力）和汇率政策等因素的影响。基于对未来投资-储蓄平衡的看法，市场对长期真实收益率的预期可能变化相当缓慢。 ↩︎

8. It is sometimes asserted that the PEH must hold because the existence of any near-term expected return differentials across bonds would imply arbitrage opportunities. This statement is only true in a theoretical risk-neutral world (which is often used in derivatives pricing); it is not true in the real world. Even though arbitrage arguments determine the levels of forward rates —— these must be consistent with spot rates according to Equation (3) —— these arguments do not say whether forward rates reflect rate expectations or required bond risk premia. Asness presents a lucid discussion on this complex issue in “OAS Models, Expected Returns, and a Steep Yield Curve” in the Journal of Portfolio Management, Summer 1993. 有时人们认为PEH必须成立，因为债券之间的任何近期预期回报差异的存在都将意味着套利机会。这一说法在理论风险中性世界（通常用于衍生品定价）中才是真实的，在现实世界中是不成立的。即使套利确定远期收益率的水平（根据等式（3），和即期收益率一致），但是这些论点并不说明远期收益率反映了收益率预期还是所需的债券风险溢价。Asness在《OAS Models, Expected Returns, and a Steep Yield Curve》（Journal of Portfolio Management, Summer 1993）对这一复杂问题进行了清晰的讨论 ↩︎

9. Because short-term bonds have very small convexity, the convexity bias is only a few basis points at maturities of less than three years. Thus, it is reasonable to ignore the bias, as an approximation, when analyzing only short-term bonds. For longer-term bonds, the rolling yields are clearly downward-biased estimates of expected returns because they ignore convexity’s significantly positive impact. This impact is probably the main explanation for the typically concave (humped) shape of the long end of the spot curve. We discuss these topics in more detail in a forthcoming report Convexity Bias and the Yield Curve. 因为短期债券的凸度非常小，期限少于3年的债券的凸度偏差只有很少的基点。因此，在分析短期债券时，忽略凸度偏差作近似是合理的。对于长期债券，滚动收益率显然是对预期回报的下偏估计，因为忽略了凸度的显著正面影响。这种影响可能是即期收益率曲线长端的典型上凸（隆起）形状的主要解释。我们在未来的报告《凸度偏差与收益率曲线》中更详细地讨论这些主题。 ↩︎

10. The finding that forwards predict the “wrong” sign for long-term rate changes is not new: it was noted in many academic studies in the 1980s (see “Literature Guide”). Moreover, Frederick Macaulay, who pioneered the concept of duration remarked on this pattern already in 1938. We must caution, however, that the estimated negative relation is not very strong for the long-term bonds, the negative correlation coefficients (the first line in Figure 7) are only about one standard deviation away from zero. The estimated correlation coefficients between $FSP_n$ and realized $BRP_n$ (the second line in Figure 7) are more significant, about two standard deviations above zero. 远期收益率预测“错误”的长期收益率变化方向的发现并不新鲜：在20世纪80年代的许多学术研究中已经注意到了（参见“文献指南”）。 此外，Frederick Macaulay（提出久期概念）在1938年就已经评论过这一模式。然而，我们必须注意的是，对于长期债券，估计的负相关性并不十分显著，相关系数(图7中的第一行)和零之间只差一个标准差。$FSP_n$和实现$BRP_n$之间的估计相关系数(图7中的第二行)更显著，距离零大约有两个标准差。 ↩︎

11. Persistence factors were discussed in Global Fixed-Immune Investments: The Persistence Effect, Martin Leibowitz, Lawrence Bader and Stanley Kogelman, Salomon Brothers Inc, February 1994. 持续性因素的讨论在《Global Fixed-Immune Investments: The Persistence Effect》（Martin Leihowitz, Lawrence Bader and Stanley Kogelman, Salomon Brothers Inc, February 1994）中 ↩︎

12. There are two main criticisms regarding the use of survey data. First, one can argue that the analyst forecasts are not “representative” of the true market expectations. Second, we do not know exactly when the rate forecasts were made; thus, the expected rate change is measured with error if we subtract a wrong base (beginning) yield from the forecast. We use midmonth rates as the base yields because, according to the Journal, most survey responses are returned around the 15th. It is not clear that either criticism should bias the forecasts systematically one way or the other and, thus, have any significant impact on the average numbers over time. 有关使用调查数据的两个主要批评。首先，人们可以认为分析师的预测对真正的市场预期不具有“代表性”。第二，我们不知道预测是何时进行的；因此，如果从预测中减去错误的基数（开始）收益率，则预期收益率变化的度量是存在误差的。我们使用月中收益率作为基准收益率，因为根据《华尔街日报》，大多数调查回复日期大约在每月15日左右。不清楚的是，哪一种批评使预测产生了系统性的偏差，并对一段时间内的平均数产生了显著的影响。 ↩︎

13. The computation is based on Equation (13) in the Appendix, adjusted for the six-month holding period. The forwards implied, on average, 106 basis points higher yield increases than the surveys. Ignoring convexity, we can approximate the impact of a 106-basis-point yield increase on bond returns by multiplying 106 with the bonds duration at horizon (for a three-month bill, “n-1” = 0.25). ($BRP_n \approx (\Delta f_{0.25} - \Delta s_{0.25}) \ast 0.25 = (80 - (-26)) \ast 0.25 = 26.5$ basis points.) This 26.5-basis-point average risk premium is the average difference between the expected six-month holding-period return of a nine-month bill and a riskless six-month bill. After annualization, we have an estimated 53-basis-point annual risk premium for a strategy of rolling over nine-month bills every six months. 计算基于附录中的等式（13），调整为六个月的持有期。平均而言，远期收益率隐含的结果比调查得到的高106个基点。忽略凸度，我们可以通过将106与期末债券久期相乘（对于三月期国库券，“n-1”=0.25）来估算106基点的收益率增长所产生的影响。（$BRP_n \approx (\Delta f_{0.25} - \Delta s_{0.25}) \ast 0.25 = (80 - (-26)) \ast 0.25 = 26.5$基点）这平均26.5个百分点的风险溢价是六月期与九月期国库券六个月持有期预期回报的平均差异。年化后，对于持有九月期国库券六个月的策略，我们估计每年有53个基点的年化风险溢价。 ↩︎

14. We discuss the empirical behavior of the bond risk premium further In forthcoming reports Does Duration Extension Enhance Long-Term Expected Returns? and Forecasting U.S. Bond Returns. 我们在随后的报告《久期增加会提高长期预期回报吗？》和《预测美国债券回报》中详细讨论债券风险溢价的经验行为。 ↩︎

15. Moreover, both measures are closely related to other measures of yield curve steepness. Equations (14) and (16) show that the forward-spot premium can he written as the sum of the term spread (or the yield difference between a long rate and a short rate. $s_n - s_1$) and the rolldown return $(n-1) \ast (s_n - s_1)$. If the spot curve is linear, the forward-spot premium will be exactly twice the term spread, Even if the curve is not linear, the forward-spot premium and the term spread are very highly correlated. Finally, many of the relations developed in this Appendix for zeros also hold approximately for coupon bonds if we substitute their durations for maturities (n), their end-of-horizon durations for n-1, and their yields for spot rates ($s_n$). 此外，这两个度量方法与收益率曲线陡峭程度的其他度量方法密切相关。等式（14）和（16）表明，远期-即期溢价可以写成期限利差（或长期与短期收益率的差，$s_n - s_1$）和下滑回报（$(n - 1) \ast (s_n - s_1)$）的总和。如果即期收益率曲线是线性的，则远期-即期溢价将是期限利差的两倍，即使曲线不是线性的，远期-即期溢价和期限利差依然高度相关。最后，如果我们把期限（n）替换成久期，把n-1替换成期末久期，以及把即期收益率（$s_n$）替换成到期收益率，那么，附录中针对零息债券得到的许多关系也将对付息债券近似成立。 ↩︎