构建可微分的衍生品定价框架

构建可微分的衍生品定价框架

上海封城期间尝试将 QuantLib 和自动微分结合起来，构建一个可微分的定价框架。

概述

在衍生品的交易和对冲中，敏感性的计算和估值同样重要，甚至更难。

计算敏感性的传统方法直接或间接地依赖差分近似，然而单纯使用差分近似在计算效率和准确性上存在明显劣势，不可避免的需要重复估值计算并引入近似误差。

若要克服差分近似的劣势，通常需要利用估值方法本身的特殊性来“特事特办”。

• 对于基于解析表达式的估值方法（例如解析解或准解析解），差分近似通常可以得到很好的近似结果，但要得到精确的结果则需要列出敏感性的解析表达式，不过这是一项艰苦的工作。
• 对于基于网格的估值方法（例如二叉树或 PDE 数值解），delta、gamma 和 theta 可以利用估值过程的中间结果计算出来。例如，在求 BSM-PDE 数值解的过程中，事实上已经得到了状态价格函数 $V(S, t)$ 的离散近似，根据离散近似建立一个平滑的插值函数拟合函数 $V(S, 0)$ 就可以算出 delta 和 gamma 的近似结果，对于 theta 来说可以根据 $V(S_0, 0)$ 和 $V(S_0, \Delta t)$ 用差分近似计算出来。不过，其他敏感性无法这样计算出来，不可避免的需要重复估值。
• 对于基于模拟的估值方法，用差分近似计算敏感性在效率和准确性上一直是个问题。固定伪随机数种子或使用拟随机数可以缓解准确性的不足，并行计算用以提高效率，此外更好的方法是用 pathwise 或 smoking adjoint（文献【1】）,直接模拟计算敏感性。

除了上述方法和技巧，近几年还流行了一种颠覆式的技术（文献【2】）——自动微分（AD），在计算估值的同时为计算敏感性留下线索（有向计算图和 Taylor 系数），试图一举解决问题。

前人工作的经验与教训

这并非是首次尝试将 QuantLib 和 AD 结合起来，目前已知 QuantLibAdjoint 是第一个吃螃蟹的人，不过这个项目看起来已经废弃了，而且结果难以复现。但前人的经验和教训依然很有价值。

经验方面，首先是 AD 框架的选择很重要，应该优先使用基于运算符重载技术的实现（文献【3】），最大限度的减少对原有代码的修改；其次，AD 框架的扩展性要强，因为除了常见函数以外，衍生品估值算法还要处理许多特殊的计算任务，例如特殊函数的计算（常见于矩匹配和随机模拟）、数值线性代数（常见于 PDE 数值解）、矩阵分解（常见于 LSMC）和复数计算（常见于 FFT），这些功能通常只能自己实现；第三，内存和对象的管理方式要和现有 QuantLib 的框架相契合；第四，要高效，否则失去了意义。

教训方面，首先是直接替换 Real 的定义是不成功的，也是不明智的。有些部分的计算没必要要求可微性，例如随机数的生成。有些部分难以实现可微性，例如计算隐含波动率（非线性函数求根）。有些算法是不可微分的，例如当前 Lagrange 插值的实现在特定点是不可微分的（需要修改实现形式才能可微）。其次，数值线性代数、矩阵分析与复数计算等模块缺失的，这将导致一大类定价引擎无法实现可微分性。第三，用日期来表示时间的做法使得直接用 AD 计算 theta 是不可能的，毕竟日期不是连续变量，不能计算微分。

选择合适的 AD 框架

AD 的实现有很多，根据已有的经验与教训最终确定了三个候选框架：

• autodiff
• Stan Math Library
• CppAD

autodiff 的扩展性强，内存和对象的管理方式也契合，但基于“表达式树”的设计使得它不适用于数值方法（例如二叉树），因为在数值方法中大量的基础计算会产生一个巨大的、几乎无法计算的表达式树。

Stan Math Library 全方面的支持衍生品估值要求的各类计算任务，但它对内存和对象的管理方式和现有 QuantLib 的框架非常不契合，具体来讲就是对原始指针采用了浅拷贝（文献【4】），这使得只有首次自动微分的计算是正确的，一旦再次赋值，结果将出现错误。

最后选择了 CppAD，但 CppAD 的短板在扩展性上。

针对欧式期权的实验

前文讲到，全局替换 Real 是不成功的，可行的策略是对每一类衍生品“解剖麻雀”并最终“各个击破”。

Maoism，Great！

以欧式期权为例，将现有的若干定价引擎修改成可微分的。

数值实验

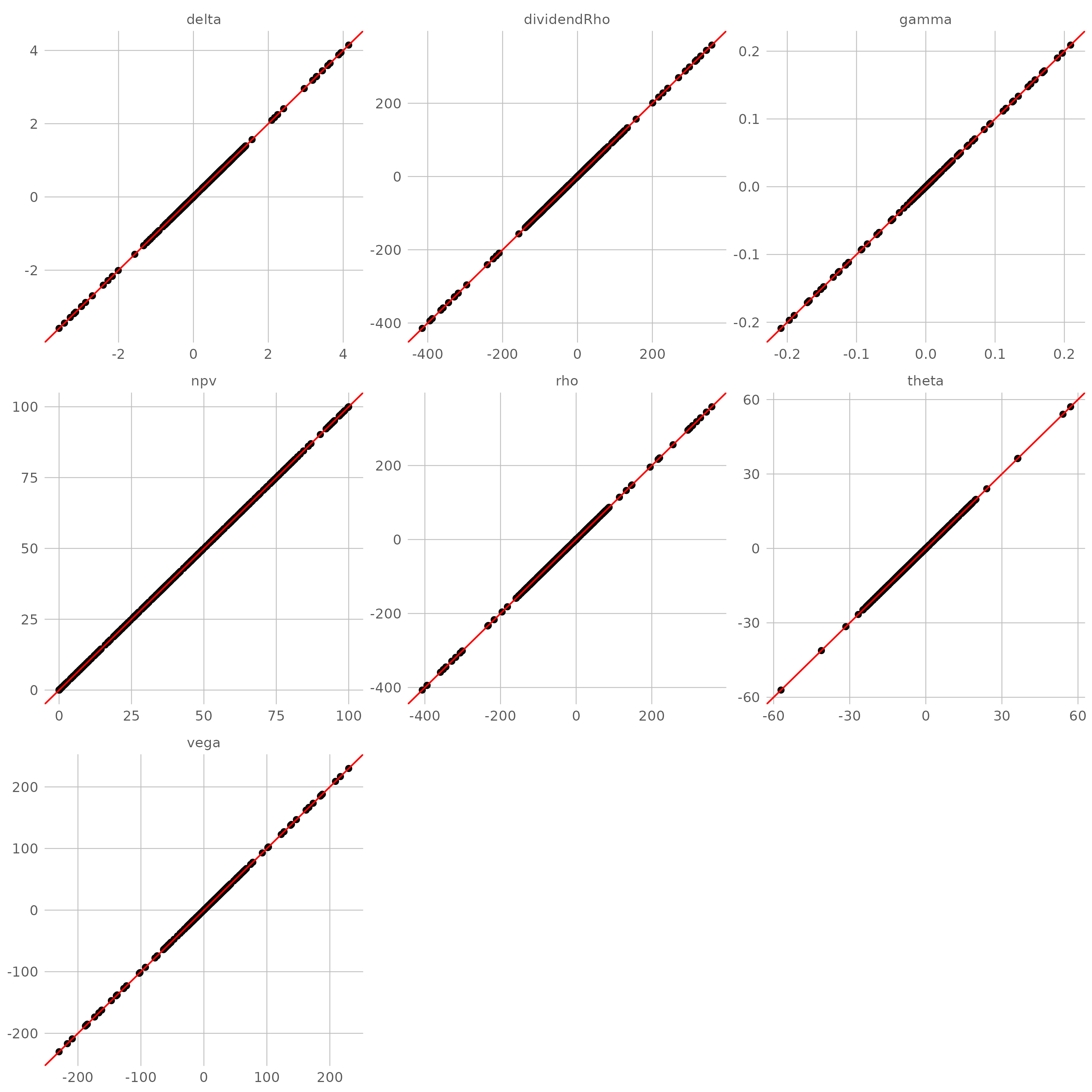
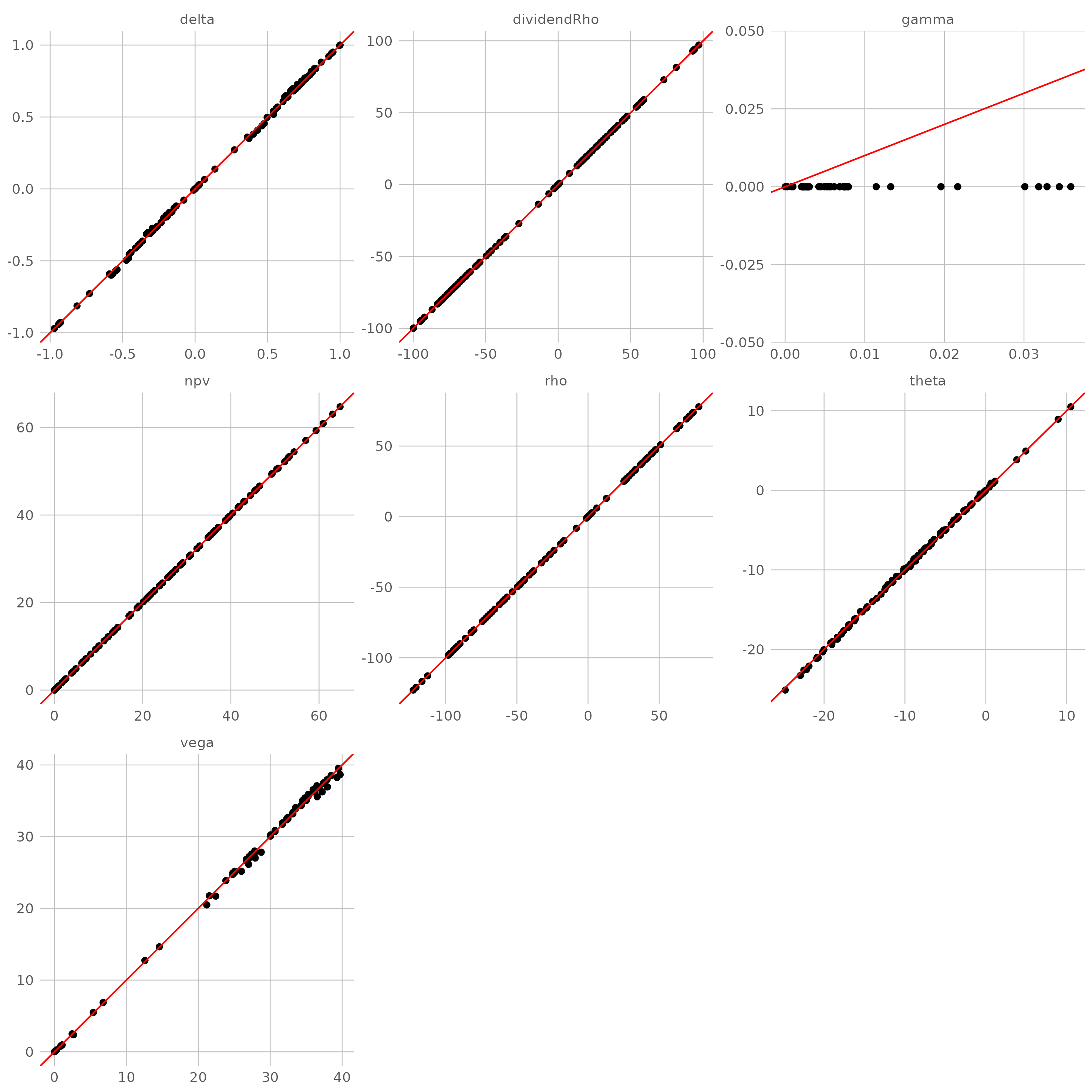
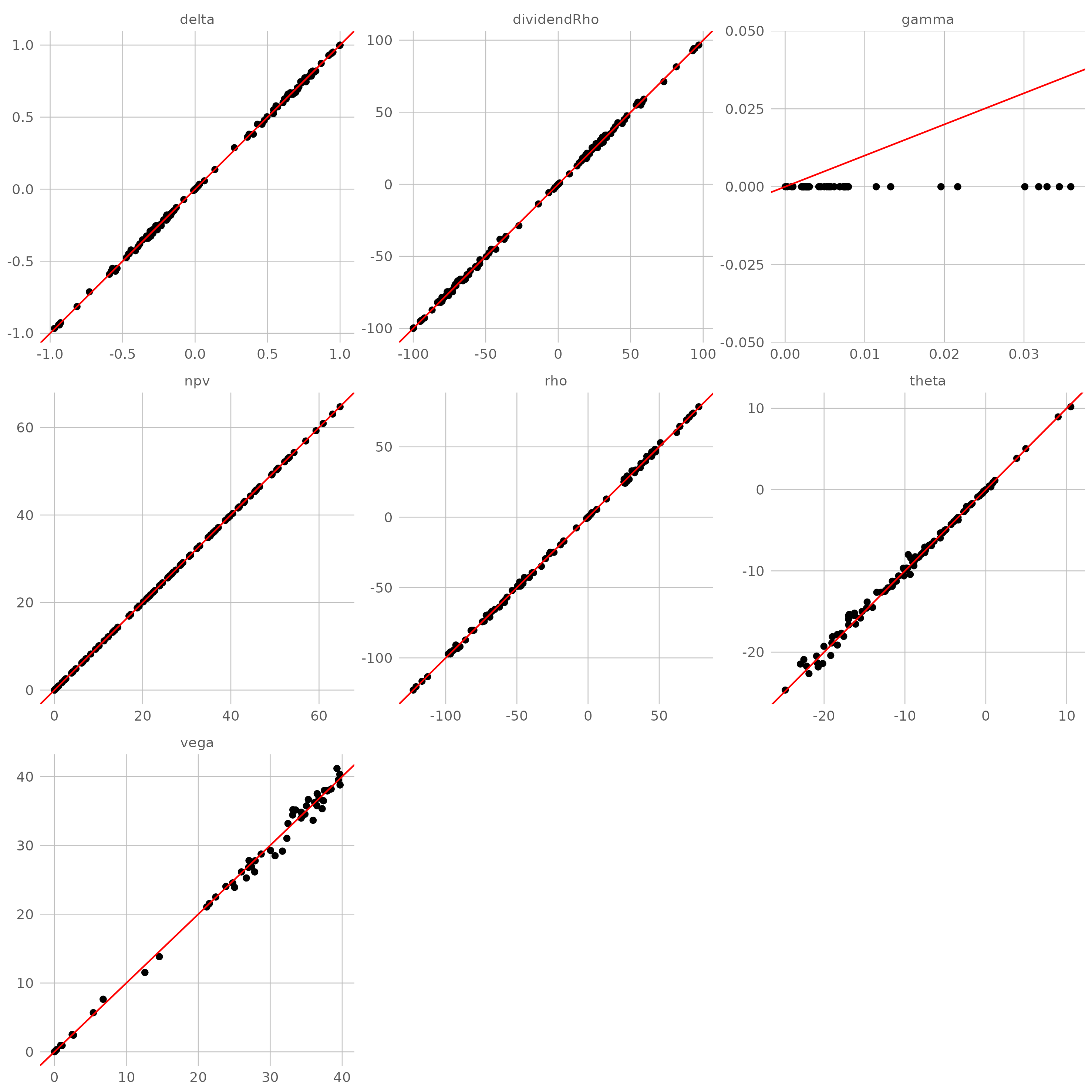
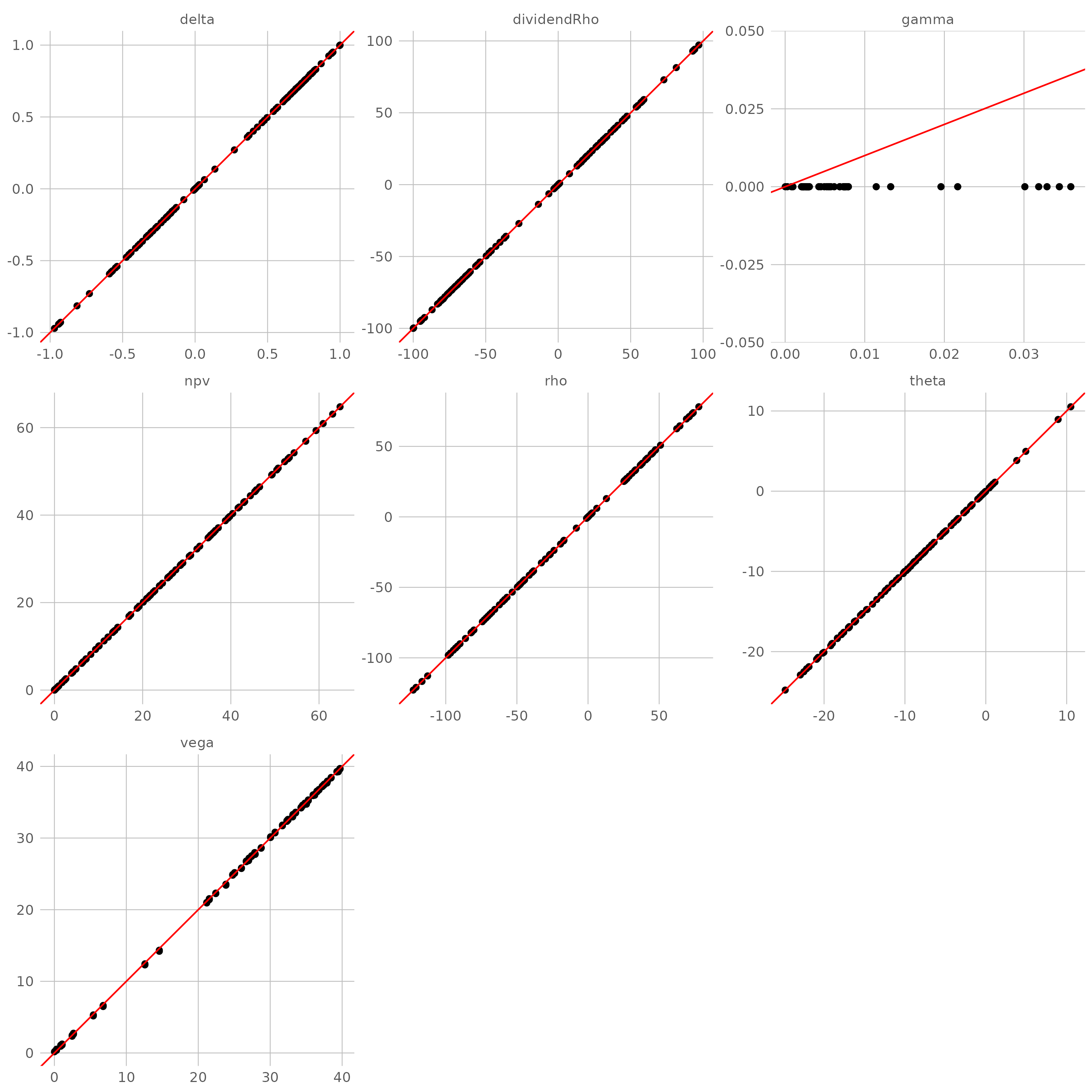
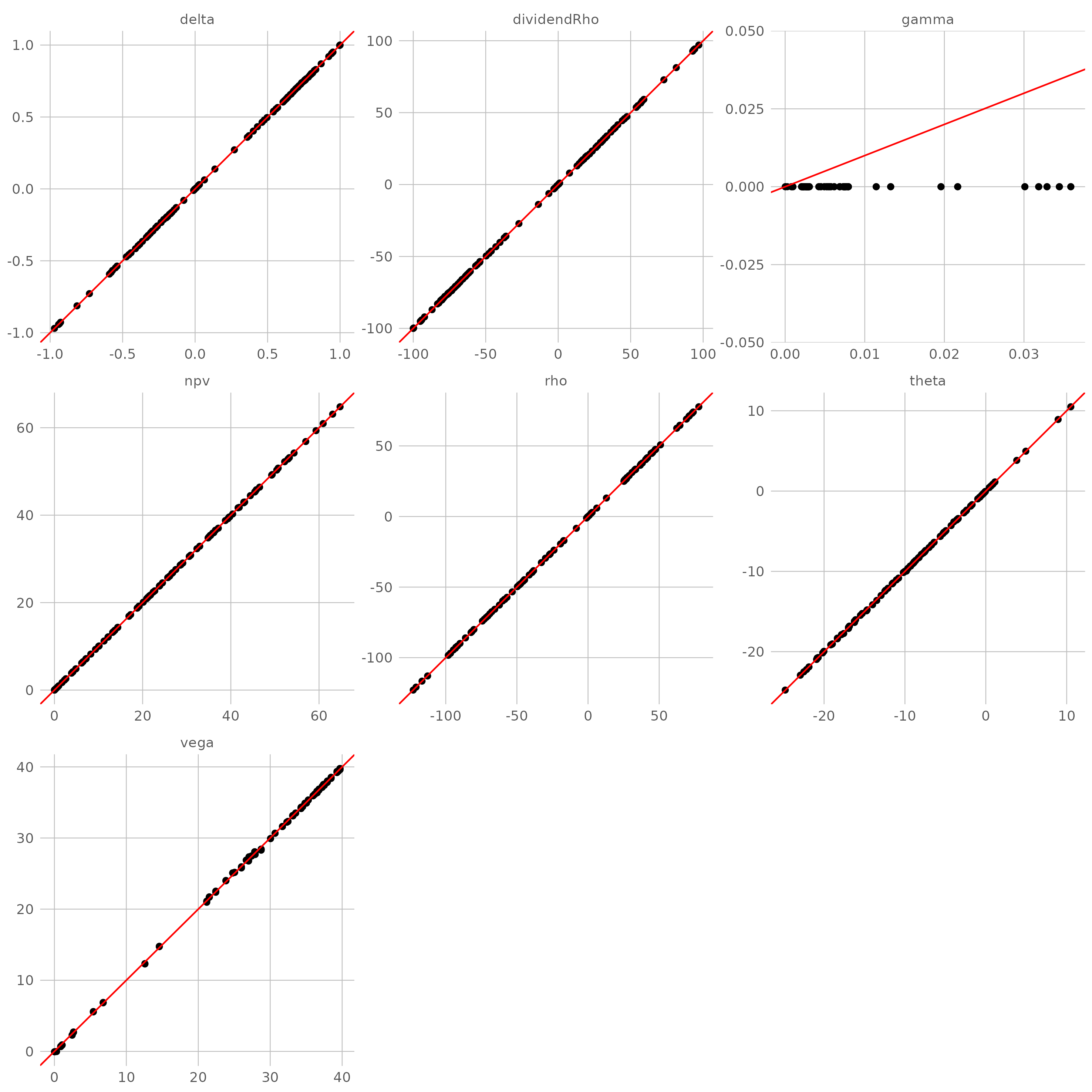
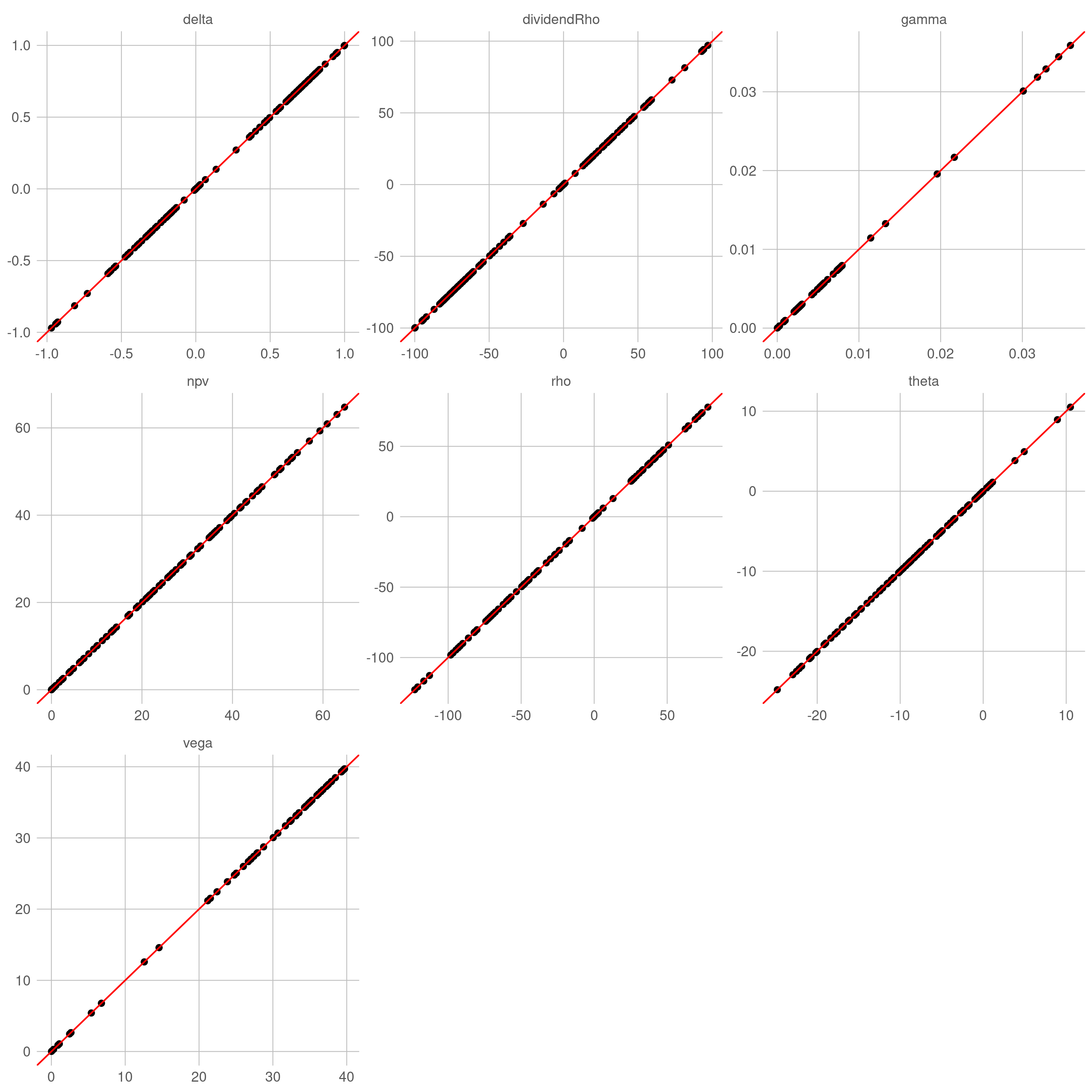
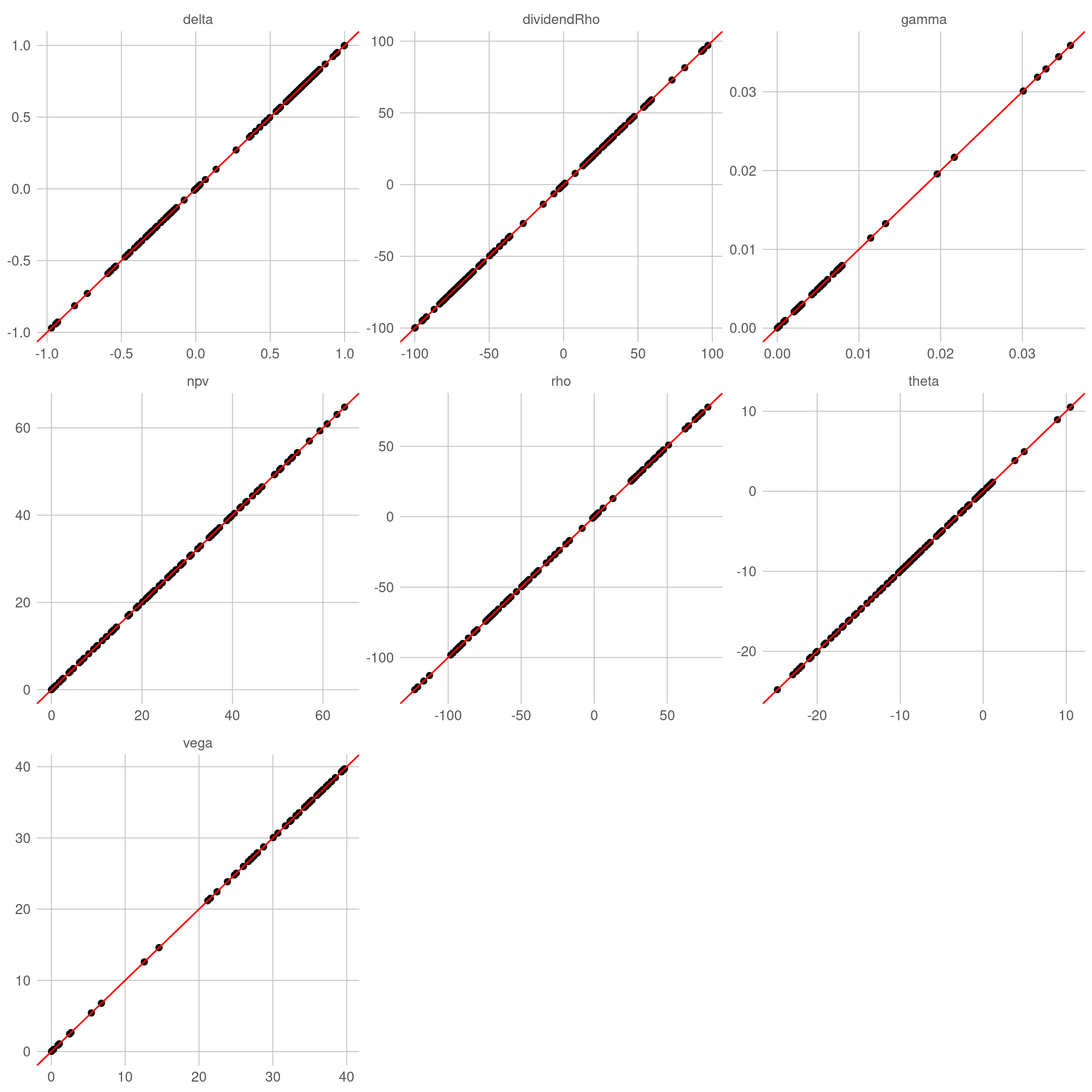
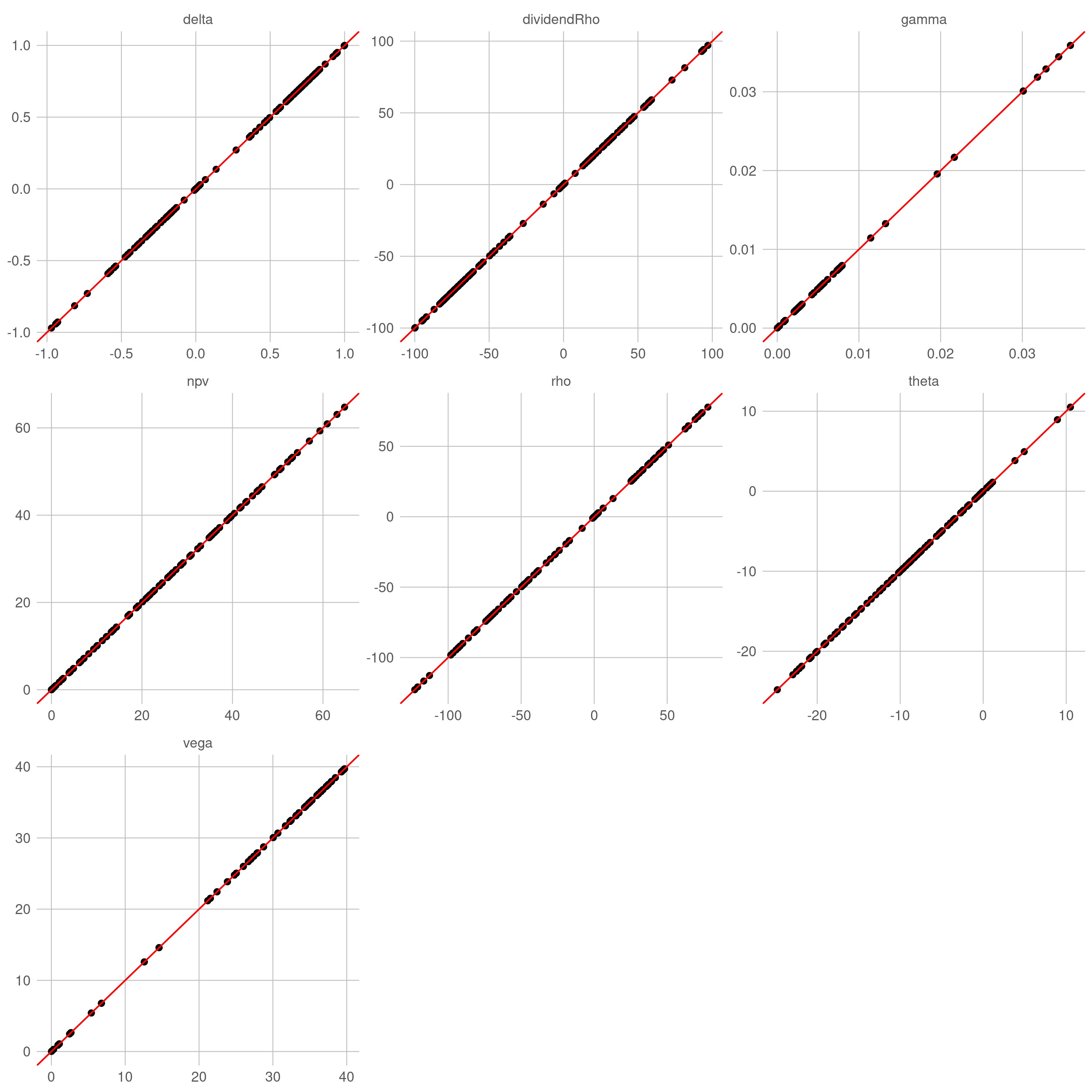
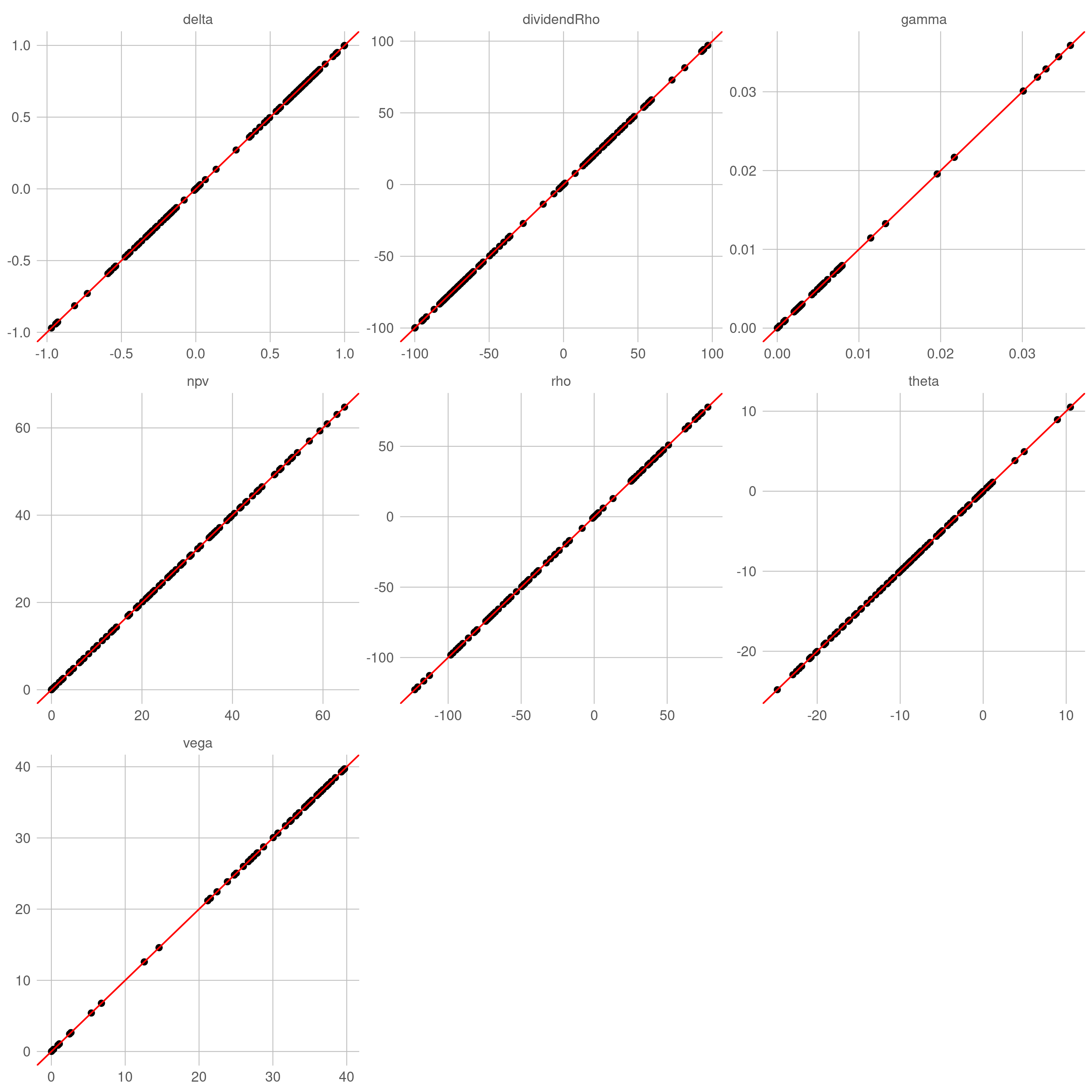
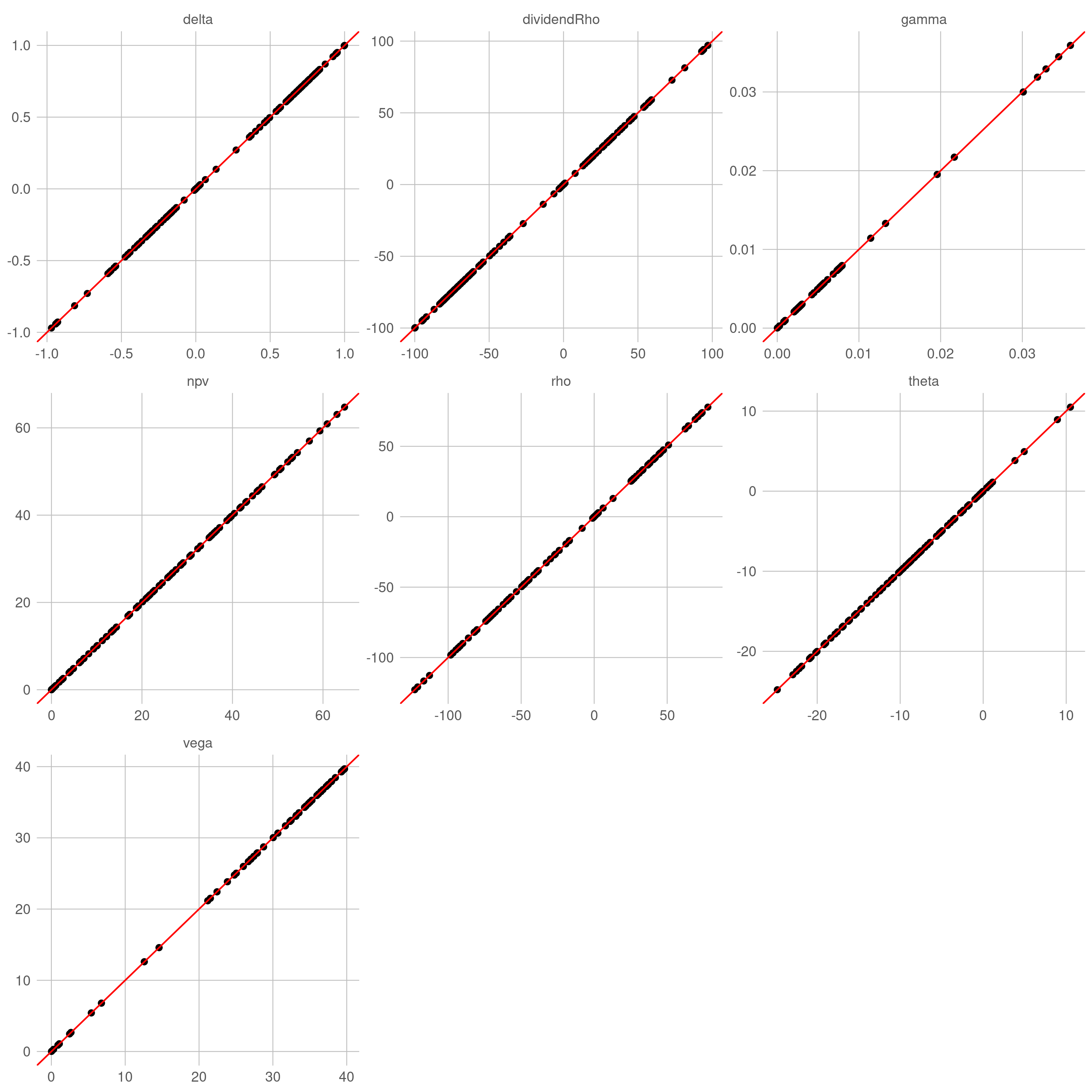
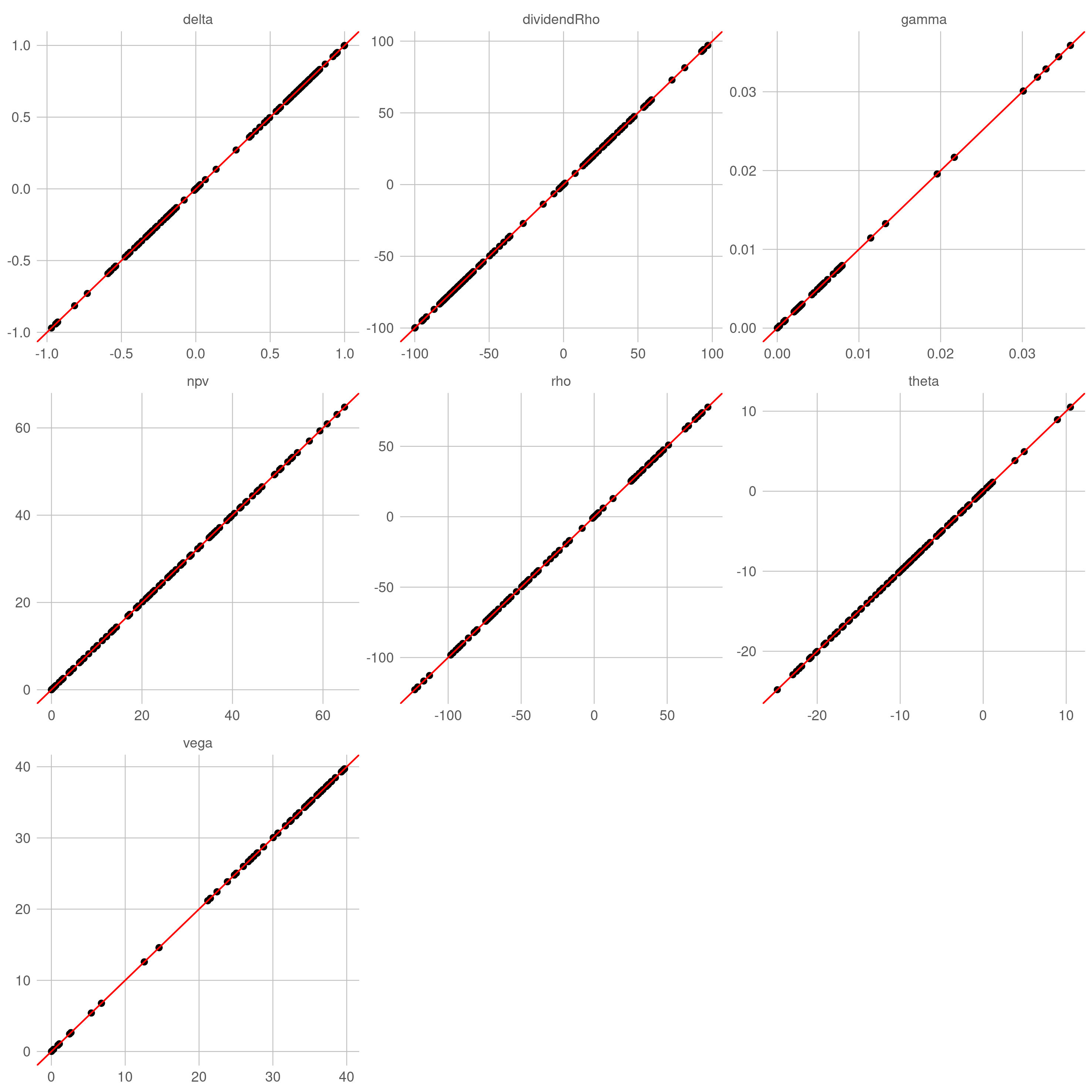
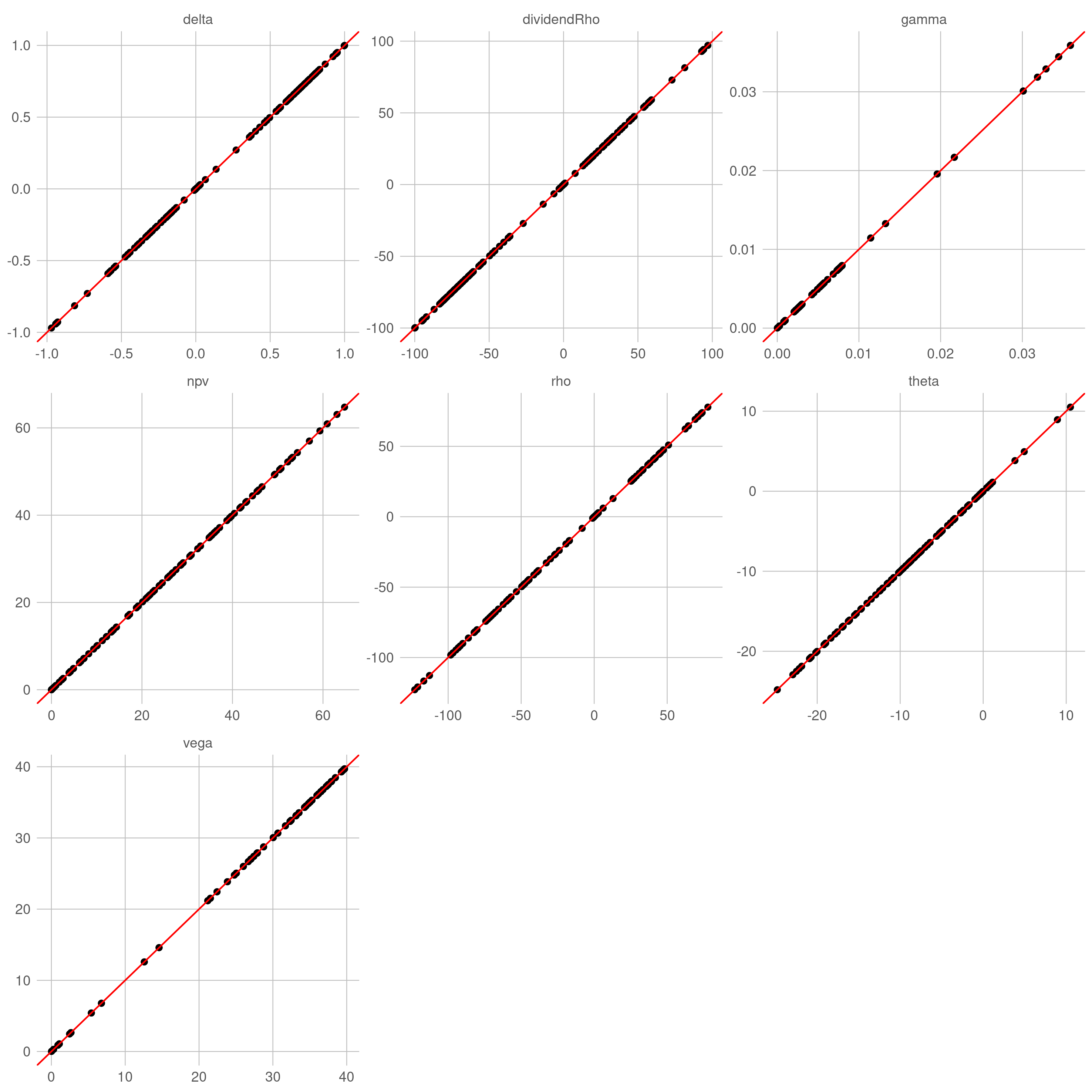
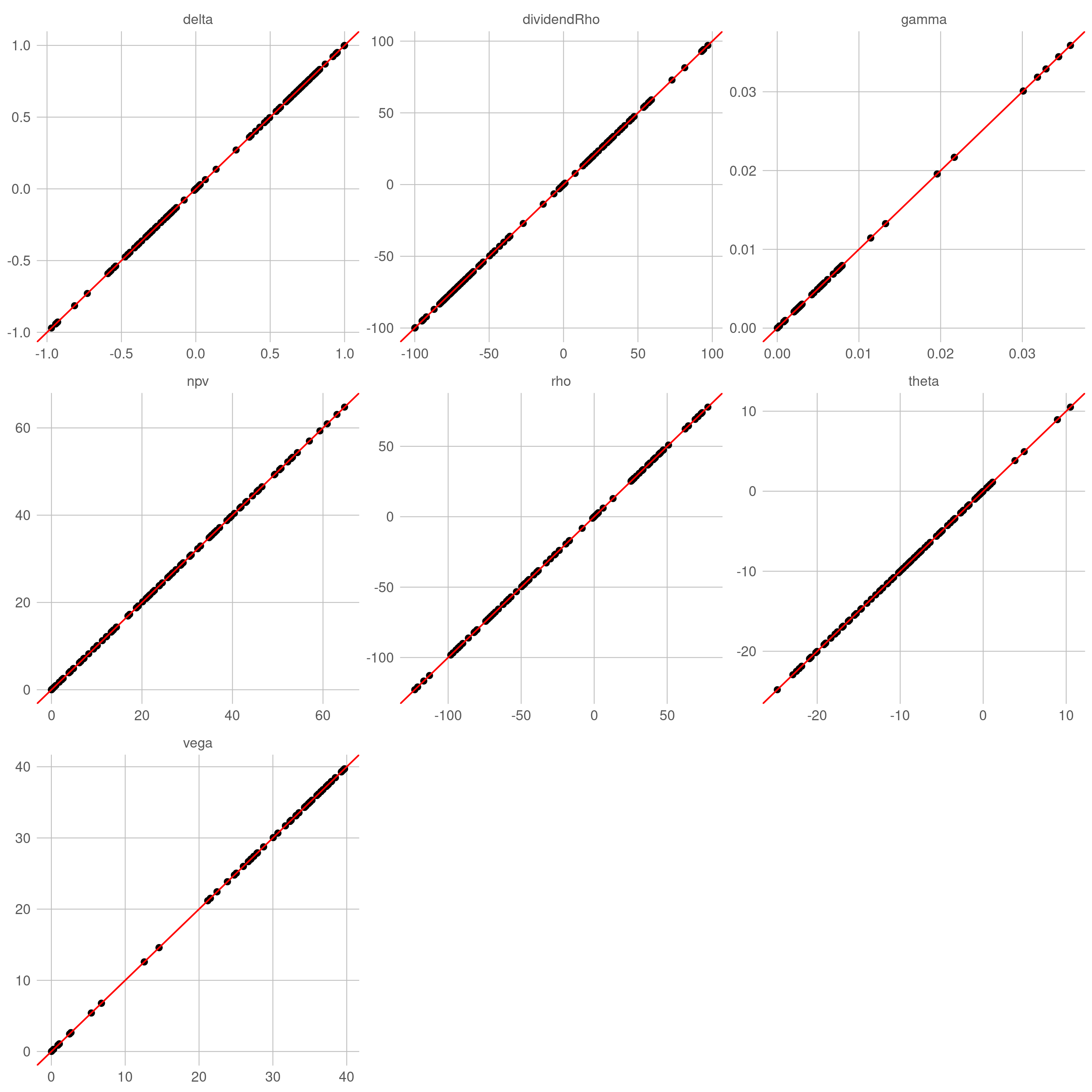
针对在不同参数组合的常系数 BSM 过程，用自动微分计算各类敏感性（目标值），并以解析公式的结果（准确值）作为比较基准。理想状态下，目标值与准确值构成的散点应该高度集中在直线 $y=x$ 附近。

解析解引擎

对于解析定价引擎，目标值与准确值之间几乎没有误差（仅有机器误差），散点完美地落在直线 $y=x$ 上。

二叉树引擎

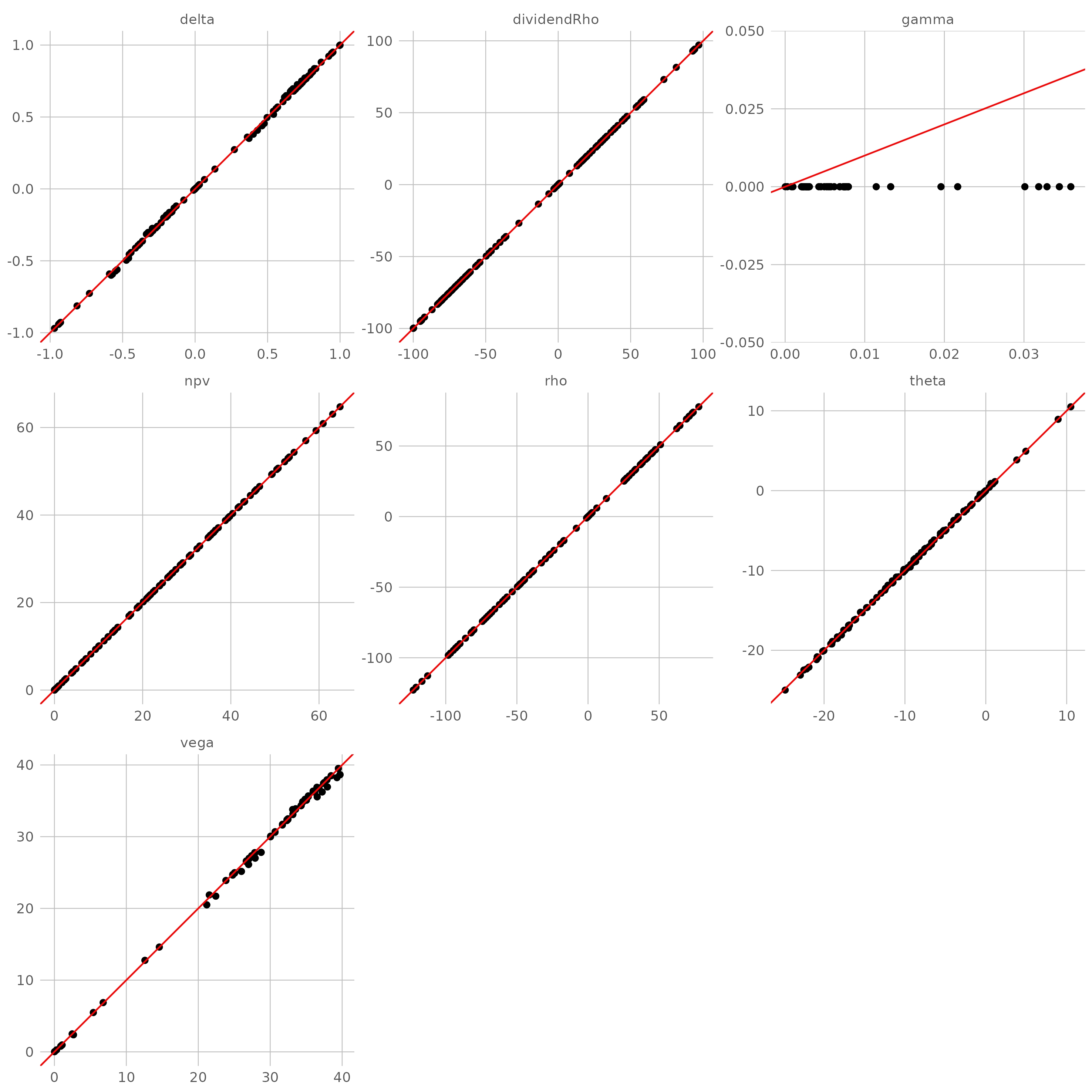
自动微分实际上是对计算机程序本身计算导数（文献【5】）。将算法想像成为一个复杂函数，二叉树自身的结构决定了这种定价方法本质上构建起一个分段线性或分段非线性的函数来近似期权定价问题的解析解，所以最终计算出的敏感性也是近似结果。此外，对于特定变量来说某些树结构建立的是一个分段线性函数，这将导致无法计算出二阶微分，下面将看到这样的例子。

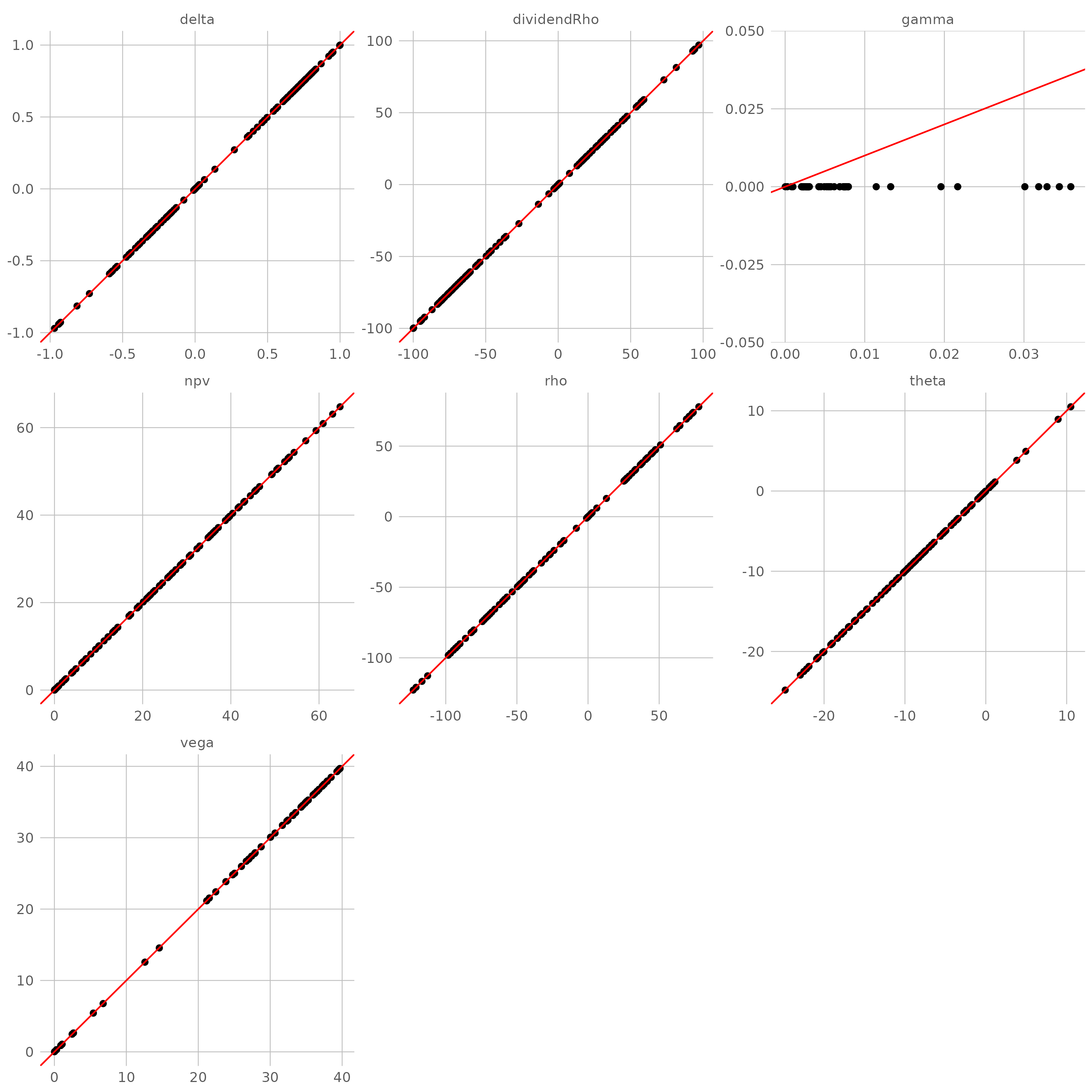
• Cox-Ross-Rubinstein 树（CRR，文献【6】）

对于最常见的 CRR 二叉树引擎，目标值与准确值之间存在微小的误差（gamma 除外），但对于价格变量来说，CRR 树本质上构建起一个分段线性函数来近似解析解，所以无法计算出二阶微分，即 gamma 全部为 0（如果分析的是数字期权，连 delta 都将是 0）。

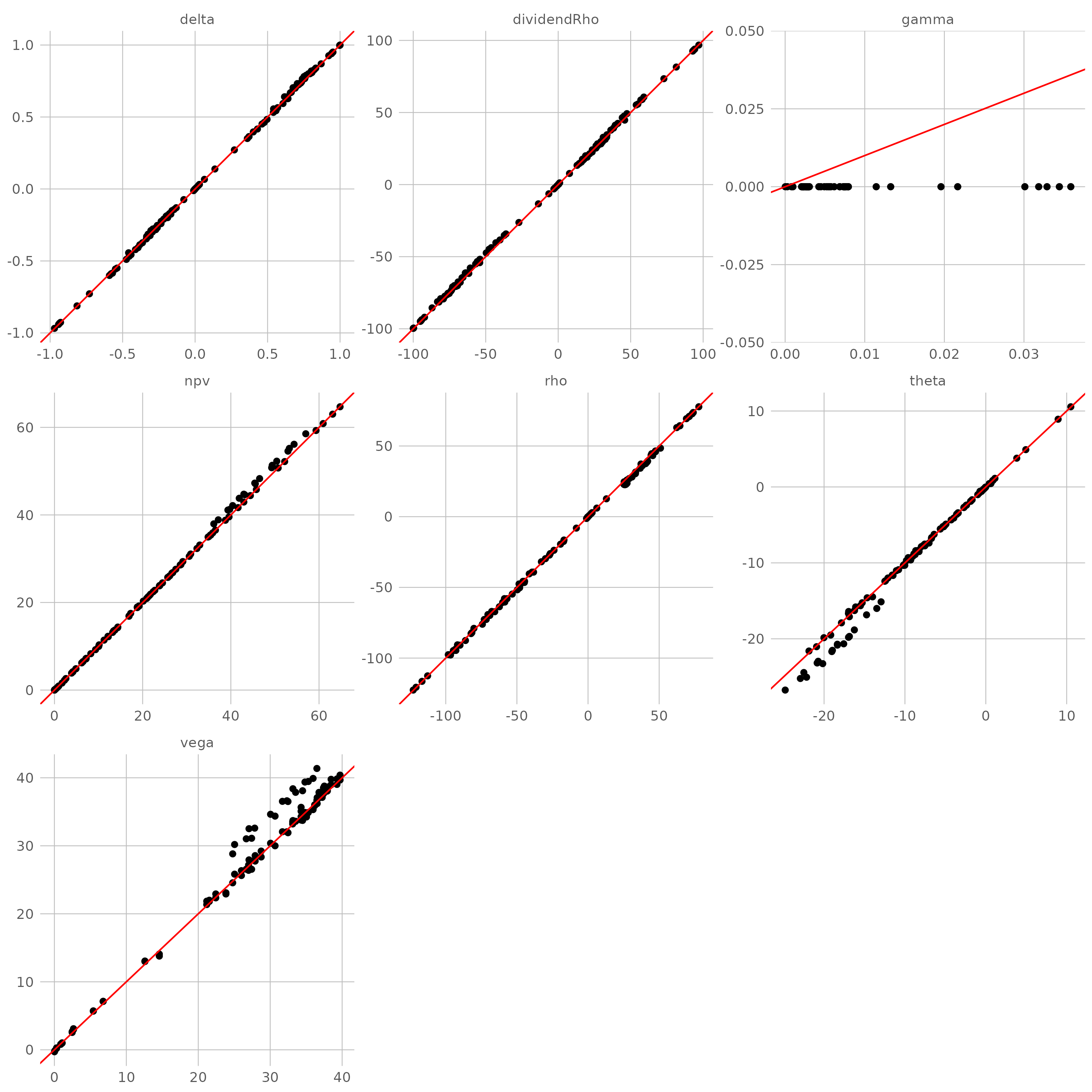
• 自适应等概率树（EQP）

EQP 树的问题和 CRR 树一致，但近似效果稍差一点。

• Joshi 树（文献【7】）

Joshi 树的近似效果非常好，同时采用了非线性近似以克服线性近似的不足，充分反映了解析解的非线性。

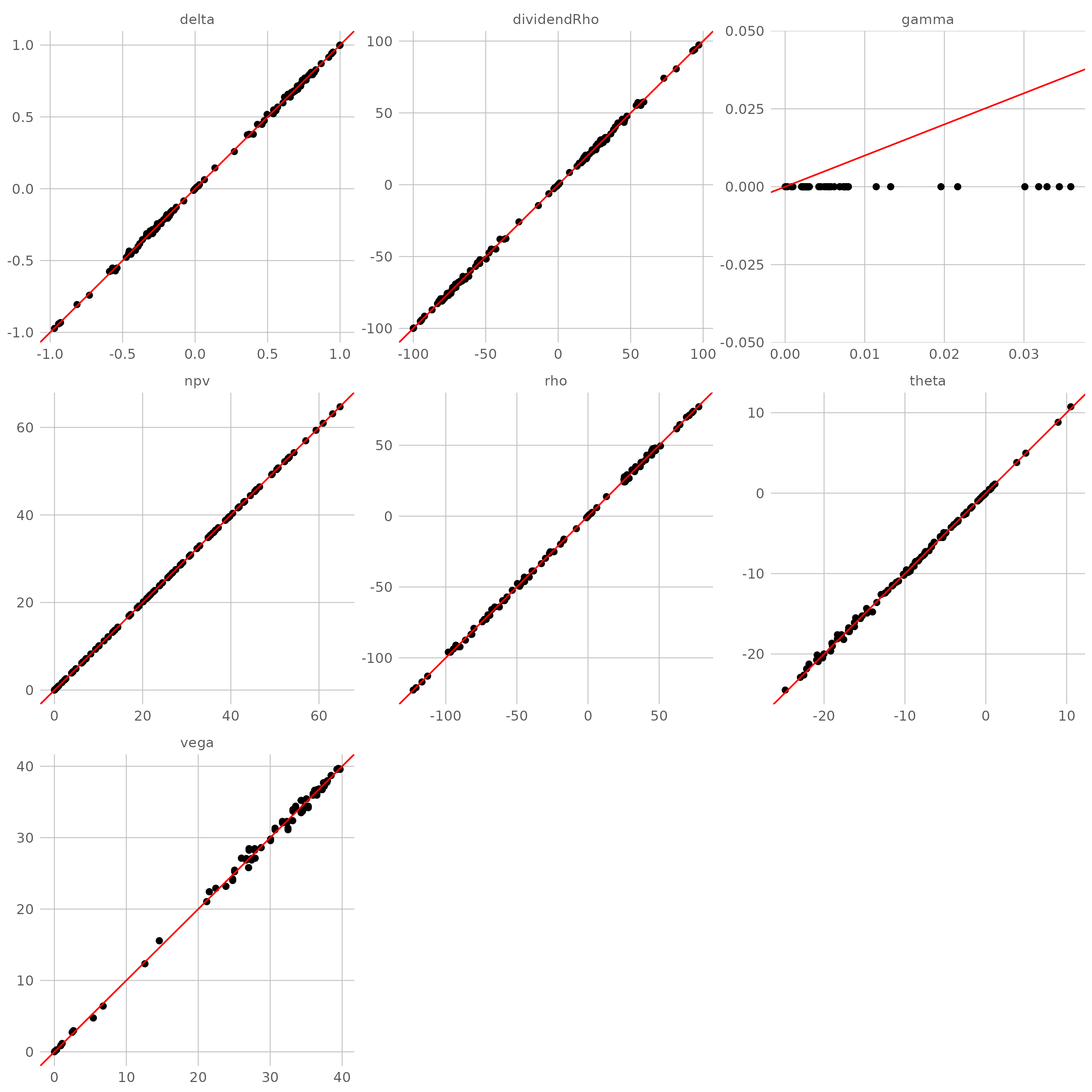
• Jarrow-Rudd 等概率树（JR，文献【8】）

JR 树的问题和 CRR 树一致。

• Leisen-Reimer 树（LR，文献【9】）

LR 树和 Joshi 树一致，也克服了线性近似的不足。

• Trigeorgis 等跳跃树（Trigeorgis，文献【10】）

Trigeorgis 树的问题和 CRR 树一致，但近似效果稍差一点。

• Tian 等跳跃树（Tian，文献【11】）

Tian 树的问题和 CRR 树一致，但近似效果稍差一点。

Monte Carlo 引擎

实际上，自动微分与随机模拟定价引擎的结合是最常见的。和某些二叉树引擎一样，对 gamma 无能为力（文献【12】）。

• 伪随机数（MC）

• 拟随机数（QMC）

有限差分引擎

自动微分与有限差分引擎的结合是最难实现的，这要求解方程组的算法和某些插值拟合算法必须是可微分的。只要保证这两点，常用的差分格式都可以保证是可微分的。

• Craig-Sneyd 格式

• Crank-Nicolson 格式

• Douglas 格式

• Hundsdorfer 格式

• 隐式 Euler 格式

• 修正 Craig-Sneyd 格式

• 修正 Hundsdorfer 格式

• Tr-BDF2 格式

最终的效果和解析解几乎一样好。

其他引擎

• FFT 引擎

AD 与傅立叶变换结合要求复数计算是可微分的，但标准库的 std::complex 模板以及相关函数通常是针对 std::complex<double> 设计的，内部的实现细节可能会破坏计算图的连续性（编译器会发出提醒），最终导致不可微分。对这类函数有必要自己实现，并用模板特化的手段绕过标准库的默认实现。

最终的效果和解析解几乎一样好。

• 积分引擎

积分引擎根据转移概率分布和支付函数直接做数值积分（梯形积分法），出现了和 CRR 树一样的问题（因为这两者的本质几乎是一致的，都可以看做是在近似计算支付函数与转移概率的内积）。

如何计算 theta？

回归问题的本源。

随着时间的“流逝”，有价证券的价值也在“变化”，theta 正是价值变化关于时间流逝的导数。可以设计一个特殊的单体——dt 来表示时间流逝，dt 在引擎内部参与估值计算，对 dt 计算自动微分就可以算出 theta，同时保留了用日期表示时间的习惯做法。

结论

以欧式期权为例，现有的若干引擎涵盖了几大类估值方法论：

• 解析公式
• 树方法（二叉树）
• 有限差分法求解 PDE
• Monte Carlo 模拟
• 傅立叶变换
• 数值积分

欧式期权的这些定价引擎可以成功的应用自动微分技术，这证明 QuantLib 剩余的部分几乎全部也可以。

尚待解决的问题

要构建完善的定价框架还有一些问题尚待解决：

• 特殊函数。大部分衍生品定价问题的解只与一个特殊函数有关——erf，标准正态分布的分布函数正是借此实现，幸运的是 CppAD 支持对 erf 求高阶导数。对于其他特殊函数（例如模拟 Heston 过程用到的 gamma 分布函数）可以参考 Stan Math Library，并用 CppAD 的原子函数机制重新实现（原子函数实现起来并不容易）。
• 矩阵分解。矩阵分解对随机模拟来说必不可少，多维 SDE 的模拟要用到 Cholesky 分解处理相关性矩阵，而 LSMC 中求解最小二乘问题同样要依赖矩阵分解技术。可微分的矩阵分解算法是自动微分领域的高级话题，幸运的是可以依赖原子函数机制高效实现。
• 求解稀疏方程组。定价问题中单因子的 PDE 数值解只需要处理一个三对角的方程组（而且存在快速算法），而多因子的 PDE 数值解则可能要求解稀疏线性系统，解稀疏方程组通常用“迭代法”求解，不难保证可微性。
• 平滑计算细节。某些算法是不可微分的（Lagrange 插值），需要重新实现。
• 平滑函数。衍生品合约的条款内涵了一些非平滑函数，例如数字期权的支付函数以及障碍期权的敲出条件。用平滑函数替代这些非平滑函数，一方面消除了不可微分的隐患，另一方面可能改善敏感性的计算结果（文献【13】）。

参考文献

【1】Smoking Adjoints: Fast Evaluation of Greeks in Monte Carlo Calculations

【2】Adjoints and Automatic (Algorithmic) Differentiation in Computational Finance

【3】A Review of Automatic Differentiation and Its Efficient Implementation

【4】The Stan Math Library: Reverse-Mode Automatic Differentiation in C++

【5】Modern Computational Finance: Aad and Parallel Simulations with Professional Implementation in C++

【6】Option Pricing: A Simplified Approach

【7】Achieving Smooth Asymptotics for the Prices of European Options in Binomial Trees

【8】Jarrow, Robert A., and Andrew Rudd. Option Pricing. Irwin, 1983.

【9】Binomial Models for Option Valuation - Examining and Improving Convergence

【10】A Log-Transformed Binomial Numerical Analysis Method for Valuing Complex Multi-Option Investments

【11】A Modified Lattice Approach to Option Pricing

【12】Monte Carlo Methods in Financial Engineering

【13】Theta (and other Greeks): Smooth Barriers