矩估计遇到神经网络

矩估计遇到神经网络

问题

先前的两篇博客文章（文 1、文 2）指出了一般大小样本量的前提下 $\text{GARCH}(1,1)$ 模型参数估计值的不稳定性，同时指出样本量极端大时估计值才趋于稳定。

但是那两篇博文仅限于指出问题，没有提供解决方案。

解决方案

通常来讲，统计模型的参数估计存在三种主要“套路”：

• 极大似然估计及其变种，通常问题最终被转化为一个数值最优化问题，前面博文中使用的 R 软件包即属于这种套路；
• 矩估计及其变种，通常问题最终被转化为一个解方程（组）的问题，方程（组）可能是非线性的，最终的估计结果可能是一个有偏估计；
• MCMC 及其变种，通常问题最终被转化为一个精心设计过的随机模拟问题。

本文的方法论遵循“矩估计”的套路，文章接下来的内容展示如何将矩估计中解（非线性）方程组这关键步转化成一个神经网络训练问题，并由此提出一个比较通用的“神经矩估计”计算框架。

$\text{GARCH}(1,1)$ 模型的神经矩估计设想

一个 $\text{GARCH}(1,1)$ 模型表示如下

\[\epsilon_t = \varepsilon_t \sigma_t \\ \sigma_t^2 = \omega + \alpha \epsilon_{t-1}^2 + \beta \sigma_{t-1}^2 \\ \varepsilon_t \sim N(0,1); \alpha, \beta \ge 0\]

$\text{GARCH}(1,1)$ 模型的神经矩估计包括以下几个步骤：

1. 随机生成一组合理的参数 $(\omega, \alpha, \beta)$；
2. 模拟一组长度为 $N$ 的样本；
3. 计算样本的一组矩 $(M_{o_1}, \dots, M_{o_m})$，其中 $o_m$ 是矩的阶数；
4. 重复第 1～3 步，得到若干矩和模拟参数的配对；
5. 以矩为输入数据、模拟参数为输出数据训练神经网络；
6. 对合理的参数的空间做网格切分；
7. 从切分中选择一组合理的参数 $(\omega_{fix}, \alpha_{fix}, \beta_{fix})$；
8. 模拟 $n$ 组长度为 $N$ 的样本；
9. 计算上述样本的矩 $(M_{o_1}^i, \dots, M_{o_m}^i), i = 1, \dots, n$；
10. 用神经网络预测上述矩对应的参数 $(\omega_{forecast}^i, \alpha_{forecast}^i, \beta_{forecast}^i), i = 1, \dots, n$；
11. 计算 $(\omega_{forecast}^i, \alpha_{forecast}^i, \beta_{forecast}^i)$ 的均值 $(\bar\omega_{forecast}, \bar\alpha_{forecast}, \bar\beta_{forecast})$
12. 遍历网格切分，得到若干 $(\omega_{fix}, \alpha_{fix}, \beta_{fix})$ 和 $(\bar\omega_{forecast}, \bar\alpha_{forecast}, \bar\beta_{forecast})$ 的配对；
13. 用多元插值描述上述 $(\bar\omega_{forecast}, \bar\alpha_{forecast}, \bar\beta_{forecast})$ 到 $(\omega_{fix}, \alpha_{fix}, \beta_{fix})$ 的经验关系。

经过上面的 13 步，一个神经矩估计框架就建好了。下面做一下解释：

• 其中第 1～4 步是为训练神经网络生成训练数据，目的是为第 5 步服务，随机生成模型参数是为了尽可能均匀地遍历参数空间。
• 第 5 步将“解方程组”转换为一个神经网络训练问题，这样的原因有两个：（1）矩 $M_{o}$ 可能是参数 $(\omega, \alpha, \beta)$ 的非线性函数，甚至得不到显式表达式；（2）从数值计算的角度看，神经网络的训练可以看作是在近似一个多维空间中的函数¹。通过训练神经网络就可以忽略 $M_{o}$ 的表达形式，以一种机械的手段近似出 $(M_{o_1}, \dots, M_{o_m})$ 与 $(\omega, \alpha, \beta)$ 的关系，达到解方程的目的，需要注意的是这里得到的是比较粗糙的近似解，不是精确解；
• 由于第 5 步得到的估计关系可能是有偏的，且不是精确解，为了比较精细地描述未知的偏差，需要得到预测结果均值和真实值之间的插值关系，第 6～13 步正是为此。

如果要估计某一组数据的 $\text{GARCH}(1,1)$ 参数需要遵循下面的步骤：

1. 确保数据的长度接近 $N$；
2. 计算一组矩 $(M_{o_1}, \dots, M_{o_m})$；
3. 用训练好的神经网络预测得到 $(\omega_{forecast}, \alpha_{forecast}, \beta_{forecast})$；
4. 通过多元插值计算最终的 $(\omega, \alpha, \beta)$，这一步主要为了纠偏。

代码实现

载入相关包。

# Packages ----

library(ggplot2)
library(fGarch)
library(keras)
library(dplyr)

配置必要的函数和对象，作为一次简化的实验，只计算三种矩，分别是：

• $M_1 = \frac{1}{N}\sum_t\vert\epsilon_t\vert = f_1(\omega, \alpha, \beta)$
• $M_2 = \frac{1}{N}\sum_t\vert\epsilon_t\vert^2 = f_2(\omega, \alpha, \beta)$
• $M_{1.5} =\frac{1}{N}\sum_t\vert\epsilon_t\vert^{1.5} = f_{1.5}(\omega, \alpha, \beta)$

# Setup ----

set.seed(123)

M1 <- function(x)
{
    sum(abs(x)) / length(x)
}

M2 <- function(x)
{
    sum(x^2) / length(x)
}

M1_5 <- function(x)
{
    sum(sqrt(abs(x)^3)) / length(x)
}

GarchCoefGenerator <- function(max_omega = 0.5,
                               up_limit = 1)
{
    omega <- runif(1, min = 0, max = max_omega)
    alpha <- runif(1)
    beta <- runif(1)

    while (alpha + beta >= up_limit)
    {
        alpha <- runif(1)
        beta <- runif(1)
    }

    return(
        list(omega = omega, alpha = alpha, beta = beta))
}

train_length <- 3000
val_length <- 1000
test_length <- 1000

train_m1 <- numeric(train_length)
train_m2 <- numeric(train_length)
train_m1_5 <- numeric(train_length)
train_omega <- numeric(train_length)
train_alpha <- numeric(train_length)
train_beta <- numeric(train_length)

val_m1 <- numeric(val_length)
val_m2 <- numeric(val_length)
val_m1_5 <- numeric(val_length)
val_omega <- numeric(val_length)
val_alpha <- numeric(val_length)
val_beta <- numeric(val_length)

test_m1 <- numeric(test_length)
test_m2 <- numeric(test_length)
test_m1_5 <- numeric(test_length)

生成训练数据。

# Train Data ----

for (i in 1:train_length)
{
    garch_coef <- GarchCoefGenerator()
    garch_sample <- garchSim(
        garchSpec(
            model = garch_coef),
        n.start = 1000, n = 1000)

    train_m1[i] <- M1(garch_sample)
    train_m2[i] <- M2(garch_sample)
    train_m1_5[i] <- M1_5(garch_sample)

    train_omega[i] <- garch_coef$omega
    train_alpha[i] <- garch_coef$alpha
    train_beta[i] <- garch_coef$beta
}

trainX <- data.frame(
    m1 = train_m1,
    m2 = train_m2,
    m1_5 = train_m1_5) %>%
    as.matrix()

trainY <- data.frame(
    omega = train_omega,
    alpha = train_alpha,
    beta = train_beta) %>%
    as.matrix()

生成验证数据。

# Val Data ----

for (i in 1:val_length)
{
    garch_coef <- GarchCoefGenerator()
    garch_sample <- garchSim(
        garchSpec(
            model = garch_coef),
        n.start = 1000, n = 1000)

    val_m1[i] <- M1(garch_sample)
    val_m2[i] <- M2(garch_sample)
    val_m1_5[i] <- M1_5(garch_sample)

    val_omega[i] <- garch_coef$omega
    val_alpha[i] <- garch_coef$alpha
    val_beta[i] <- garch_coef$beta
}

valX <- data.frame(
    m1 = val_m1,
    m2 = val_m2,
    m1_5 = val_m1_5) %>%
    as.matrix()

valY <- data.frame(
    omega = val_omega,
    alpha = val_alpha,
    beta = val_beta) %>%
    as.matrix()

用 keras 构建神经网络。

# Model Training ----

model <- keras_model_sequential()

model %>%
    layer_dense(
        units = 9,
        input_shape = c(3),
        activation = 'sigmoid') %>%
    layer_dense(
        units = 3,
        activation = 'sigmoid') %>%
    compile(
        loss = 'mae',
        optimizer = 'adam')

summary(model)

实验采用了结构非常简单的神经网络结构，一个两层的多元感知机，超参数、激活函数和优化方法没有调优。

__________________________________________________________________________
Layer (type)                     Output Shape                 Param #     
==========================================================================
dense_1 (Dense)                  (None, 9)                    36          
__________________________________________________________________________
dense_2 (Dense)                  (None, 3)                    30          
==========================================================================
Total params: 66
Trainable params: 66
Non-trainable params: 0
__________________________________________________________________________

训练。

history <- model %>%
    fit(
        trainX,
        trainY,
        validation_data = list(
            valX, valY),
        batch_size = 50,
        epochs = 1000)

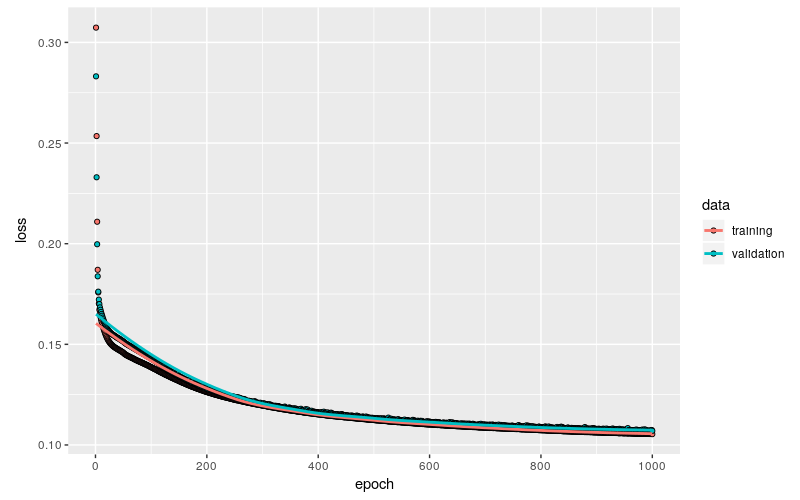
plot(history)

训练结果非常理想，训练集和验证集上的 loss 基本上同步衰减到 0.11 左右，并且从趋势上看大约已经接近了极限水平。

延续前面两篇博文的主题，将 $\text{GARCH}(1,1)$ 的模型参数限定为 $(0.2,0.2,0.2)$，生成测试数据，后面要测试估计值的稳定性，以及是否有偏。

# Test ----

for (i in 1:test_length)
{
    garch_coef <- list(
        omega = 0.2, alpha = 0.2, beta = 0.2)

    garch_sample <- garchSim(
        garchSpec(
            model = garch_coef),
        n.start = 1000, n = 1000)

    test_m1[i] <- M1(garch_sample)
    test_m2[i] <- M2(garch_sample)
    test_m1_5[i] <- M1_5(garch_sample)
}

predictX <- data.frame(
    m1 = test_m1,
    m2 = test_m2,
    m1_5 = test_m1_5) %>%
    as.matrix()

预测结果。

predictY <- model %>%
    predict(predictX) %>%
    as.data.frame()

predictY$idx <- 1:nrow(predictY)

colnames(predictY) <- c('omega', 'alpha', 'beta', 'idx')

head(predictY)

      omega     alpha      beta idx
1 0.1946828 0.1991726 0.2187224   1
2 0.1677427 0.2192231 0.2021861   2
3 0.1989923 0.2052666 0.2165215   3
4 0.1739261 0.2159361 0.2049208   4
5 0.1766528 0.2010799 0.2137308   5
6 0.2087296 0.1955684 0.2248684   6

目前预测结果看起来还不错。

验证估计结果

用红线代表估计值的均值，蓝线代表理论值。

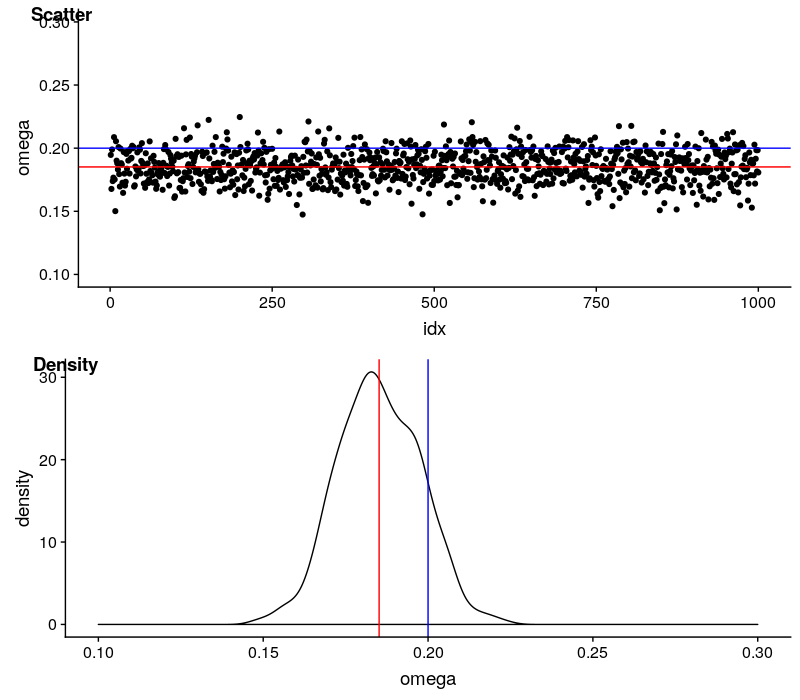
$\omega$

fig_scatter <- ggplot(
    data = predictY) +
    geom_point(
        mapping = aes(
            x = idx, y = omega)) +
    geom_hline(yintercept = 0.2, color = 'blue') +
    geom_hline(yintercept = mean(predictY$omega), color = 'red') +
    ylim(c(0.1, 0.3))

fig_scatter

fig_density <- ggplot(
    data = predictY) +
    geom_density(
        mapping = aes(
            x = omega)) +
    geom_vline(xintercept = 0.2, color = 'blue') +
    geom_vline(xintercept = mean(predictY$omega), color = 'red') +
    xlim(c(0.1, 0.3))

fig_density

plot_grid(
    fig_scatter, fig_density,
    nrow = 2, labels = c('Scatter', 'Density'))

$\omega$ 的估计值非常稳定，变动区间也很小。估计是有偏的，估计值会系统性地低估真实值，差距在 0.015 左右。

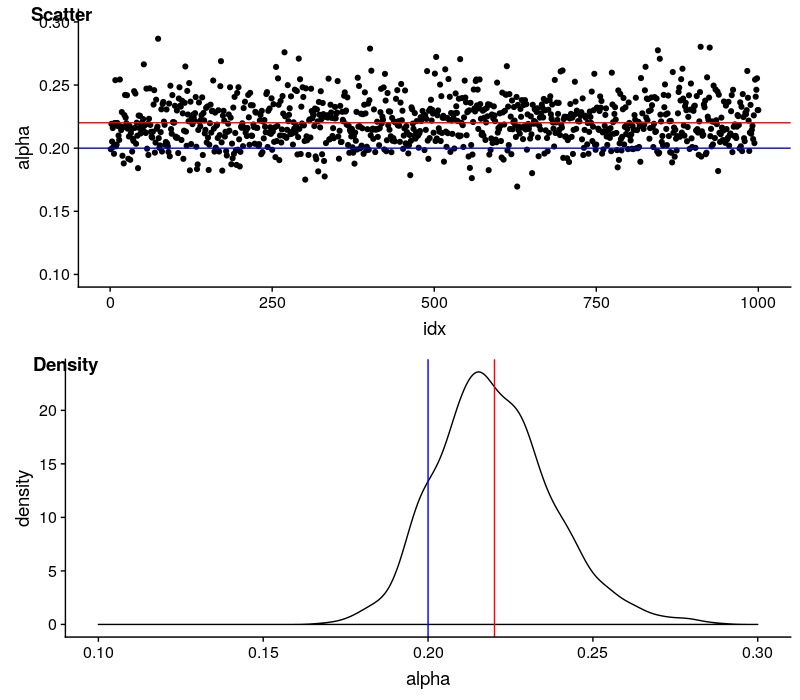
$\alpha$

fig_scatter <- ggplot(
    data = predictY) +
    geom_point(
        mapping = aes(
            x = idx, y = alpha)) +
    geom_hline(yintercept = 0.2, color = 'blue') +
    geom_hline(yintercept = mean(predictY$alpha), color = 'red') +
    ylim(c(0.1, 0.3))

fig_scatter

fig_density <- ggplot(
    data = predictY) +
    geom_density(
        mapping = aes(
            x = alpha)) +
    geom_vline(xintercept = 0.2, color = 'blue') +
    geom_vline(xintercept = mean(predictY$alpha), color = 'red') +
    xlim(c(0.1, 0.3))

fig_density

plot_grid(
    fig_scatter, fig_density,
    nrow = 2, labels = c('Scatter', 'Density'))

$\alpha$ 的估计值非常稳定，变动区间也很小。估计是有偏的，估计值会系统性地高估真实值，差距在 0.02 左右。

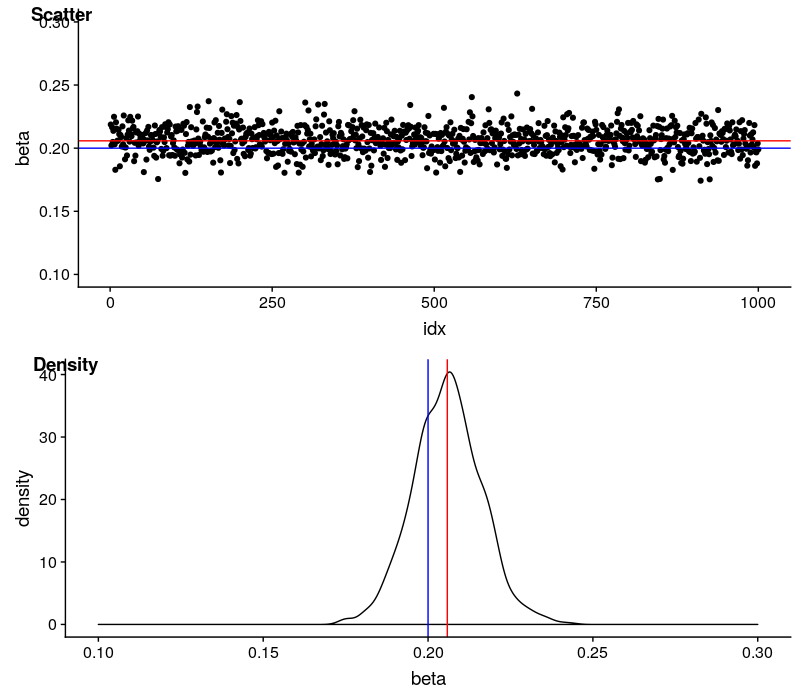
$\beta$

fig_scatter <- ggplot(
    data = predictY) +
    geom_point(
        mapping = aes(
            x = idx, y = beta)) +
    geom_hline(yintercept = 0.2, color = 'blue') +
    geom_hline(yintercept = mean(predictY$beta), color = 'red') +
    ylim(c(0.1, 0.3))

fig_scatter

fig_density <- ggplot(
    data = predictY) +
    geom_density(
        mapping = aes(
            x = beta)) +
    geom_vline(xintercept = 0.2, color = 'blue') +
    geom_vline(xintercept = mean(predictY$beta), color = 'red') +
    xlim(c(0.1, 0.3))

fig_density

plot_grid(
    fig_scatter, fig_density,
    nrow = 2, labels = c('Scatter', 'Density'))

$\beta$ 的估计值非常稳定，变动区间也很小。估计是有偏的，估计值会系统性地高估真实值，差距在 0.006 左右，已经很小了。

一个悬而未决的理论问题

从工程的角度看，前面的实践是没问题的，但有一个理论问题悬而未决，那就是样本矩的存在性。一个潜在的论证思路如下：

1. 研究 $\text{GARCH}(1,1)$ 过程 $\epsilon_t$ 矩的存在条件；
2. 论证过程 $\vert\epsilon_t\vert^o(1 \le o \le 2)$ 的遍历性；
3. 结合以上两点，用 $\epsilon_t$ 矩的存在性加上 $\vert\epsilon_t\vert^o$ 的遍历性证明样本矩的存在性。

$\text{GARCH}(1,1)$ 模型矩的统计性质

$\text{GARCH}(1,1)$ 过程 $\epsilon_t$ 存在 $2m$ 阶矩的充分必要条件是²

\[\mu(\alpha, \beta, m) = \sum_{j=0}^m C_m^j a_j \alpha^j \beta^{m-j} < 1\]

其中，$m$ 是正整数；$a_0=1$，$a_j = \prod_{i=1}^j (2i-1), j = 1,\dots,m$。

如果要求 $\epsilon_t$ 有 4 阶矩，即 $m = 2$，那么

\[(\alpha + \beta)^2 + 2\alpha^2 < 1\]

模型参数的取值范围比较狭小，仅局限在原点为中心的一个椭圆内。

如果放松要求，让 $\epsilon_t$ 仅有 2 阶矩，即 $m = 1$，那么

\[\alpha + \beta < 1\]

这已经是普通 $\text{GARCH}(1,1)$ 模型能达到的最大范围了，如果 $\alpha + \beta = 1$，模型将变为没有二阶矩的 $\text{I-GARCH}(1,1)$ 模型。

$\text{GARCH}(1,1)$ 模型的遍历性

目前还没有找到合适的文献，可能需要在 $\alpha + \beta < 1$ 的基础上在近一步缩小取值范围。

如果读者中有人对此问题有较深入的见解，请不吝赐教，我的邮箱是：xuruilong100@163.com

结论

受限于个人家用电脑的计算能力，我的数值实验只能做到这一步，毕竟框架的后半部分是一个计算密集型任务。

我对目前的试验结果很满意，神经矩估计在一般大小样本上表现出的稳定性远超基于极大似然方法论的经典方法，对于工程实践来说，现在到达的计算准确度基本够用了。

对于样本矩的存在性还需要进一步的研究。

如果有足够的计算能力验证框架的后半部分是有效且实用的，神经矩估计方法有潜力推广成为一个估计复杂统计（随机）模型参数的普适框架。

参考文献

1. 《Neural Networks and Deep Learning》（Michael Nielsen） ↩︎

2. 《协整理论与波动模型（第二版）》（张士英、樊智），定理 6-4 ↩︎