MACD 的数学解释

MACD 的数学解释

MACD 的一般定义

\[\begin{align*} DIF &= EMA(P, w_{fast}) - EMA(P,w_{slow}) \\ DEM &= EMA(DIF, w_{signal}) \\ BAR &= 2 \times (DIF - DEM) \end{align*}\]

引入延迟算子

将 $w$ 定义为 $EMA$ 的衰减系数，即

\[EMA_t = (1-w) \cdot P_t + w \cdot EMA_{t-1}\]

将 $L$ 定义为“延迟算子”，公式重写成：

\[EMA_t = \frac{1-w}{1-wL} P_t\]

进而推导出：

\[\begin{align*} DIF_t &= \left( \frac{1-w_{fast}}{1-w_{fast}L} - \frac{1-w_{slow}}{1-w_{slow}L} \right) P_t \\ DEM_t &= \frac{1-w_{signal}}{1-w_{signal}L} P_t \\ BAR_t &= 2\cdot DIF_t \frac{w_{signal}(1-L)}{1-w_{signal}L} \\ &= 2 \cdot \frac{w_{signal}(1-L)}{1-w_{signal}L} \cdot \frac{(w_{slow} - w_{fast})(1-L)}{(1-w_{slow}L)(1-w_{fast}L)} P_t \end{align*}\]

下面解析 $BAR_t$ 的计算中，历史数据的权重。

Taylor 展开

采用最通常的参数配置 $MACD(12,26,9)$，即

\[\begin{align*} w_{fast} &= (12-1) / (12+1) = 11/13 \\ w_{slow} &= (26-1) / (26+1) = 25/27 \\ w_{signal} &= (9-1) / (9+1) = 8/10 = 4/5 \end{align*}\]

要得到历史数据在公式中的权重，必须对分数形式算子做 Taylor 展开，得到多项式级数的表达形式。将上述参数代入到公式中：

\[BAR_t =2 \cdot \frac{4/5(1-L)}{1-4/5L} \cdot \frac{(25/27 - 11/13)(1-L)}{(1-25/27L)(1-11/13L)} P_t\]

在网站 WolframAlpha 上找到 Taylor 展开，输入上述公式

taylor series 2*(4/5*(1-x))/(1-4/5*x) * ((25/27 - 11/13)*(1-x))/((1-25/27*x)*(1-11/13*x))

得到 Taylor 展开的解析形式：

\[f(L) = \sum_{n=0}^{\infty} \frac{32\left(819(\frac{4}{5})^n - 765(\frac{11}{13})^n + 65(\frac{25}{27})^n \right)}{29835} L^n\]

所以，历史数据 $P_{t-n}$ 的权重是：

\[\frac{32\left(819(\frac{4}{5})^n - 765(\frac{11}{13})^n + 65(\frac{25}{27})^n \right)}{29835}\]

权重分析

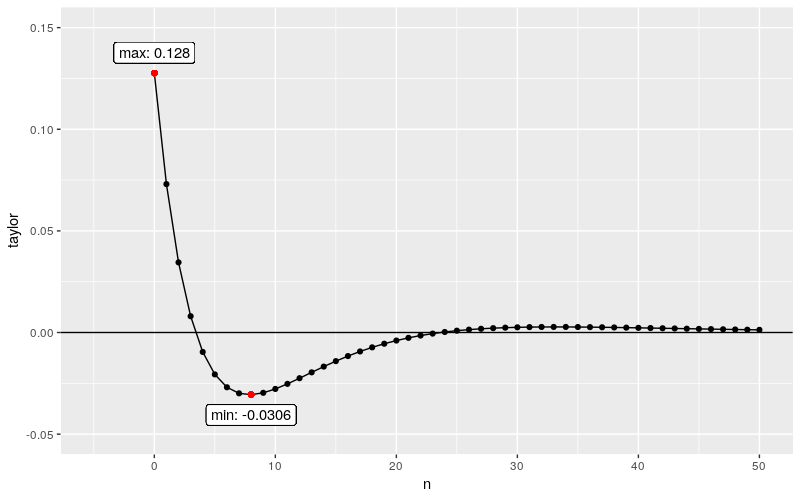
画出前 50 个历史数据的权重

整体来看，权重的分布为三段：

1. 近期的数据赋予正的权重，但迅速衰减
2. 中期的数据赋予负的权重，绝对值先增后减
3. 远期的数据权重几乎为 0

$MACD$ 中的 $BAR$ 基本上可以看作是近期数据与中期数据的差。

共振？

如图，采用最通常的参数配置 $MACD(12,26,9)$，最大权重出现在 $n=0$ 时，最小权重出现在 $n=8$ 时。如果价格序列体现出“波浪”的形态，一个波谷到邻近波峰之间索引的差值等于 $8-0$，按照上述权重的分布，基本上可以断定这时的 $BAR$ 同时达到了最大值，因为我们为波分和波谷分别赋予了最大和最小的权重。也就是说，价格序列波浪的长度大致等于最大最小权重对应索引的差时，价格序列和 $BAR$ 将出现“共振”。

启发

根据前文的分析，MACD 指标其实是历史数据的加权值，只不过权重序列复杂一点吧了。那么，可以直接从“权重序列”出发，重新设计技术分析指标，相比于调整传统技术指标的“参数”，基于权重序列设计出的指标具有更大的灵活性。