QuantLib 金融计算——利率曲线之构建曲线(3)
介绍用 QuantLib 基于样本券的交易数据估算出即期利率的期限结构。
由于版本问题,代码可能与最新版不兼容。
QuantLib 金融计算——利率曲线之构建曲线(3)
载入 QuantLib 和其他包:
1
2
3
4
5
6
import QuantLib as ql
import seaborn as sb
import numpy as np
import pandas as pd
print(ql.__version__)
1
1.15
概述
本文展示利用 quantlib-python 根据样本券的交易数据估算出即期利率的期限结构的完整流程,并指出当前实现所存在的问题。
示例所用的样本券交易数据来自专门进行期限结构分析的 R 包——termstrc。具体来说是数据集 govbonds 中的 GERMANY 部分,包含 2008-01-30 这一天德国市场上 52 只固息债的成交数据。
注意:为了适配 QuantLib,实际计算中删除了两只债券的数据,以保证所有样本券的到期时间均不相同。样本券数据在附录中列出。
估算期限结构的步骤
QuantLib 中估算期限结构的核心流程有两步:
- 配置
*Helper对象,描述样本券信息,包括付息时间表(schedule)、价格(默认用净价)、票息等; - 配置期限结构模型,可以额外提供样本券权重、优化方法、参数正则化条件等参数辅助计算。
读取样本券数据
1
2
3
4
5
6
7
8
9
10
11
12
13
govBond = pd.read_csv(
'GERMANY_INFO.csv',
parse_dates=['MATURITYDATE', 'ISSUEDATE'])
numberOfBonds = govBond.shape[0]
PRICE = [
ql.QuoteHandle(ql.SimpleQuote(p)) for p in govBond['PRICE']]
MATURITYDATE = [
ql.Date(m.day, m.month, m.year) for m in govBond['MATURITYDATE']]
ISSUEDATE = [
ql.Date(i.day, i.month, i.year) for i in govBond['ISSUEDATE']]
COUPONRATE = govBond['COUPONRATE'].values
一些基本配置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 查看 govbonds 数据集可知样本券均为每年付息一次
frequency = ql.Annual
# termstrc 的日期计算并不如 QuantLib 精细,
# 为了和 termstrc 的算法保持一致,示例使用如下天数计算规则
dc = ql.Actual365Fixed(ql.Actual365Fixed.Standard)
paymentConv = ql.Unadjusted
terminationDateConvention = ql.Unadjusted
convention = ql.Unadjusted
redemption = 100.0
faceAmount = 100.0
# 其实我不知道样本券所在的交易所,
# 所以不确定是不是该用这个日历 :)
calendar = ql.Germany(ql.Germany.Eurex)
# 估值日期 2008-01-30
today = calendar.adjust(ql.Date(30, 1, 2008))
ql.Settings.instance().evaluationDate = today
# 为了和 termstrc 的算法保持一致,示例采用 T+0 结算
bondSettlementDays = 0
bondSettlementDate = calendar.advance(
today,
ql.Period(bondSettlementDays, ql.Days))
配置 *Helper 对象
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
instruments = []
for j in range(numberOfBonds):
# 配置付息时间表
schedule = ql.Schedule(
ISSUEDATE[j],
MATURITYDATE[j],
ql.Period(frequency),
calendar,
convention,
terminationDateConvention,
ql.DateGeneration.Backward,
False)
# 配置 Helper 对象
# 因为样本券均为固息债,所以采用 FixedRateBondHelper 类
# 对于其他金融工具,需要使用对应的 Helper 类
helper = ql.FixedRateBondHelper(
PRICE[j],
bondSettlementDays,
faceAmount,
schedule,
[COUPONRATE[j]],
dc,
paymentConv,
redemption)
instruments.append(helper)
配置期限结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
tolerance = 1.0e-6
max = 5000
# 即期利率的 Svensson 模型
sf = ql.SvenssonFitting()
# 即期利率的 Nelson Siegel 模型
nsf = ql.NelsonSiegelFitting()
# 用指数样条函数拟合贴现因子
esf = ql.ExponentialSplinesFitting()
# 用简单多项式函数拟合贴现因子
spf = ql.SimplePolynomialFitting(8)
# 用三次 B-样条函数拟合贴现因子
knots = [-20.0, -10.0, 0.0, 0.25, 0.5, 1, 3, 5, 10, 20, 30, 40, 50]
cbsf = ql.CubicBSplinesFitting(knots)
tsSvensson = ql.FittedBondDiscountCurve(
bondSettlementDate, instruments, dc,
sf,
tolerance, max)
tsNelsonSiegel = ql.FittedBondDiscountCurve(
bondSettlementDate, instruments, dc,
nsf,
tolerance, max)
tsExponentialSplines = ql.FittedBondDiscountCurve(
bondSettlementDate, instruments, dc,
esf,
tolerance, max)
tsSimplePolynomial = ql.FittedBondDiscountCurve(
bondSettlementDate, instruments, dc,
spf,
tolerance, max)
tsCubicBSplines = ql.FittedBondDiscountCurve(
bondSettlementDate, instruments, dc,
cbsf,
tolerance, max)
估算期限结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
sv = []
ns = []
es = []
sp = []
cbs = []
matList = []
matDate = bondSettlementDate
while matDate <= bondSettlementDate + ql.Period(31, ql.Years):
matDate = matDate + ql.Period(1, ql.Days)
matList.append(
dc.yearFraction(bondSettlementDate, matDate))
sv.append(
tsSvensson.zeroRate(matDate, dc, ql.Continuous, frequency).rate() * 100)
ns.append(
tsNelsonSiegel.zeroRate(matDate, dc, ql.Continuous, frequency).rate() * 100)
es.append(
tsExponentialSplines.zeroRate(matDate, dc, ql.Continuous, frequency).rate() * 100)
sp.append(
tsSimplePolynomial.zeroRate(matDate, dc, ql.Continuous, frequency).rate() * 100)
cbs.append(
tsCubicBSplines.zeroRate(matDate, dc, ql.Continuous, frequency).rate() * 100)
汇总结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 以 termstrc 的估算结果作为比较基准
beta0 = 5.017052
beta1 = -1.117214
beta2 = -3.173622
tau = 2.443936
termstrc = [
beta0 + \
beta1 * (1 - np.exp(-m / tau)) / (m / tau) + \
beta2 * ((1 - np.exp(-m / tau)) / (m / tau) - np.exp(-m / tau)) for m in matList]
df = pd.DataFrame(
dict(
maturity=matList * 6,
rate=sv + ns + es + sp + cbs + termstrc,
type=np.repeat(
['Svensson', 'NelsonSiegel', 'ExponentialSplines',
'SimplePolynomial', 'CubicBSplines', 'termstrc'], len(matList))))
print(tsSvensson.fitResults().solution())
print(tsNelsonSiegel.fitResults().solution())
print(tsExponentialSplines.fitResults().solution())
print(tsSimplePolynomial.fitResults().solution())
print(tsCubicBSplines.fitResults().solution())
print(tsSvensson.fitResults().minimumCostValue())
print(tsNelsonSiegel.fitResults().minimumCostValue())
print(tsExponentialSplines.fitResults().minimumCostValue())
print(tsSimplePolynomial.fitResults().minimumCostValue())
print(tsCubicBSplines.fitResults().minimumCostValue())
sb.relplot(
x='maturity', y='rate', kind='line', hue='type',
size='type', sizes=[2, 2, 2, 2, 2, 4],
data=df, height=5, aspect=1.6)
1
2
3
4
5
6
7
8
9
10
11
[ -134.509; 134.548; 136.375; -0.0234826; 0.000905134; 0.422332 ]
[ -9.7222; 9.75752; 38.0528; 3.14624e-05 ]
[ -31238.6; -95904.4; 46747.5; 53652; 21350.9; 2438.62; -77566.2; 36236.2; 0.000302241 ]
[ -0.0373576; 0.00165862; -0.000203106; 9.83472e-06; -1.47693e-07 ]
[ 1.13572; 0.977843; 0.948002; 0.90216; 0.798218; 0.616569; 0.355499; 0.293158 ]
0.00032255014803192505
0.0020683101877706977
0.0019235041138322383
0.0008108667989534623
0.00037198366450668654
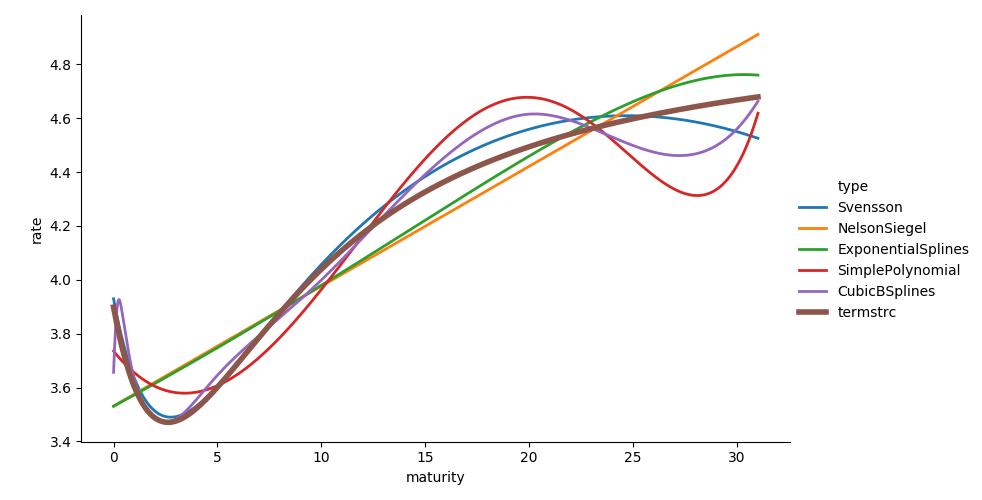
图 1:QuantLib 的结果
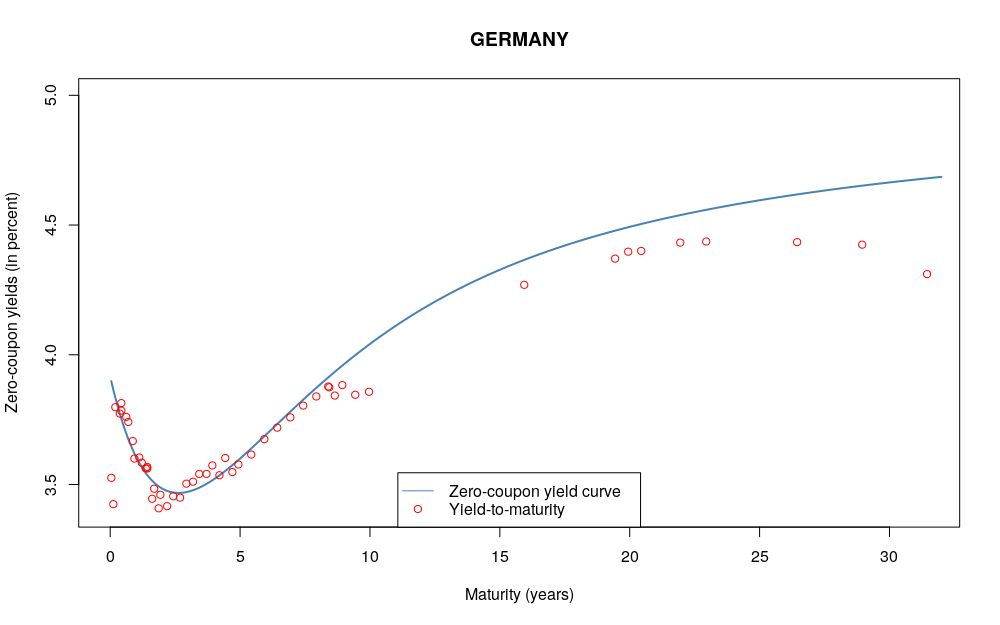
图 2:termstrc 的结果
注意:尽管以 termstrc 的结果作为基准,并不意味着基准就是正确答案。
NelsonSiegel、SimplePolynomial 和 ExponentialSplines 的结果与基准相去甚远。Svensson 和 CubicBSplines 的结果在短端与基准非常接近,但在长端依然有明显差距,Svensson 和 CubicBSplines 的结果要略低于基准。
考虑到基准似乎在长端高估了真实利率水平,Svensson 和 CubicBSplines 的结果可能要好于基准。另外,CubicBSplines 甚至顾及到了 0 附近的两个“异常值”。
当前实现存在的问题与对策
粗看结果似乎还可以接受,但实际上经不起推敲。
- 首先,根据 Nelson Siegel 模型和 Svensson 模型的经济意义(参考文献【1】),估计结果绝对值的数量级应该和利率处于同一水平,通常是 10 以内的某个数。尤其是模型中的 $\beta_0$,大致应该等于利率的平均值。
- 其次,三次 B-样条的结果在远端出现了 S 形的扭曲,可能是 knot 选择不当的结果,最终结果对 knot 的选择其实非常敏感(参考文献【3】)。另外,QuantLib 采用了 $d(t) = \sum_{i=0}^{n} c_i \times N_{i,3}(t)$ 的格式($N_{i,3}(t)$ 是基本样条函数,$d(t)$ 是贴现因子),因为 $N_{i,3}(t)$ 在最外测的两个 knot 上取值非常小(MATLAB 的演示),这使得使用者必须提供而外的 knot 完全覆盖当前的期限范围才能有合理的估计,相当反人类的设计。
- 第三,指数样条等方法的参数过于极端。
所有问题的根源是相同的,因为估算期限结构本质上是一个优化问题。以 Nelson Siegel 模型和 Svensson 模型为例,参数估计本身是一个相当有挑战性的非凸优化问题(参考文献【2】),可能需要借助一些特殊的技术手段(参考文献【2】),而不是依赖于某个优化算法。但是 quantlib-python 在封装期限结构接口的时候只保留了样本券权重一个自由度,优化算法、正则化条件等选项均被忽略,特别是优化算法,统一使用比较原始的单纯形算法。
若要改良当前的结果,一种方法是编写 C++ 程序使用其他优化算法,并配置正则化条件;另一种方法是自定义 swig 的接口文件,修改 quantlib-python 期限结构类的接口,使其能使用其他优化算法,并接受正则化条件。
如果无法实现以上两种方法,在当前有限的条件下推荐使用三次 B-样条函数估算期限结构,但要注意 knot 的选择。
参考文献
【1】《收益率曲线的建模和预测——基于 DNS 方法创新》,东北财经大学出版社
【2】R. Ferstl and J. Hayden, “Zero-Coupon Yield Curve Estimation with the Package termstrc” Journal of Statistical Software, August 2010, Volume 36, Issue 1.
【3】James, J. and N. Webber, “Interest Rate Modelling” John Wiley, 2000.
附录
样本券数据。
| ISIN | MATURITYDATE | ISSUEDATE | COUPONRATE | PRICE | ACCRUED |
|---|---|---|---|---|---|
| DE0001141414 | 2008-02-15 | 2002-08-14 | 0.0425 | 100.002 | 4.087 |
| DE0001137131 | 2008-03-14 | 2006-03-08 | 0.03 | 99.92 | 2.6557 |
| DE0001141422 | 2008-04-11 | 2003-04-11 | 0.03 | 99.805 | 2.4262 |
| DE0001137149 | 2008-06-13 | 2006-05-30 | 0.0325 | 99.75 | 2.069 |
| DE0001135077 | 2008-07-04 | 1998-07-04 | 0.0475 | 100.305 | 2.7514 |
| DE0001137156 | 2008-09-12 | 2006-08-30 | 0.035 | 99.76 | 1.3579 |
| DE0001141430 | 2008-10-10 | 2003-09-25 | 0.035 | 99.75 | 1.0902 |
| DE0001137164 | 2008-12-12 | 2006-11-30 | 0.0375 | 99.975 | 0.5225 |
| DE0001135101 | 2009-01-04 | 1999-01-04 | 0.0375 | 100.0416 | 0.2869 |
| DE0001137172 | 2009-03-13 | 2007-02-28 | 0.0375 | 100.0574 | 3.3299 |
| DE0001141448 | 2009-04-17 | 2004-02-02 | 0.0325 | 99.5049 | 2.5751 |
| DE0001137180 | 2009-06-12 | 2007-05-30 | 0.045 | 101.0971 | 2.877 |
| DE0001135127 | 2009-07-04 | 1999-07-04 | 0.045 | 101.137 | 2.6066 |
| DE0001137198 | 2009-09-11 | 2007-08-24 | 0.04 | 100.7199 | 1.5628 |
| DE0001141455 | 2009-10-09 | 2004-08-25 | 0.035 | 99.8883 | 1.0997 |
| DE0001137206 | 2009-12-11 | 2007-09-21 | 0.04 | 100.908 | 0.5683 |
| DE0001135135 | 2010-01-04 | 1999-10-22 | 0.05375 | 103.3553 | 0.4112 |
| DE0001141463 | 2010-04-09 | 2005-02-24 | 0.0325 | 99.5034 | 2.6462 |
| DE0001135150 | 2010-07-04 | 2000-05-05 | 0.0525 | 103.913 | 3.041 |
| DE0001141471 | 2010-10-08 | 2005-08-26 | 0.025 | 97.4229 | 0.7923 |
| DE0001135168 | 2011-01-04 | 2000-09-29 | 0.0525 | 104.5636 | 0.4016 |
| DE0001141489 | 2011-04-08 | 2006-02-26 | 0.035 | 99.7527 | 2.8593 |
| DE0001135184 | 2011-07-04 | 2001-05-23 | 0.05 | 104.3708 | 2.8962 |
| DE0001141497 | 2011-10-14 | 2006-08-30 | 0.035 | 99.6051 | 1.0519 |
| DE0001135192 | 2012-01-04 | 2001-12-28 | 0.05 | 104.8603 | 0.3825 |
| DE0001141505 | 2012-04-13 | 2007-02-28 | 0.04 | 101.3415 | 3.3661 |
| DE0001135200 | 2012-07-04 | 2002-06-26 | 0.05 | 105.29 | 2.8962 |
| DE0001141513 | 2012-10-12 | 2007-08-24 | 0.0425 | 102.4969 | 1.4631 |
| DE0001135218 | 2013-01-04 | 2002-12-31 | 0.045 | 103.7602 | 0.3443 |
| DE0001135234 | 2013-07-04 | 2003-06-24 | 0.0375 | 100.2803 | 2.1721 |
| DE0001135242 | 2014-01-04 | 2003-10-21 | 0.0425 | 102.6046 | 0.3251 |
| DE0001135259 | 2014-07-04 | 2004-04-25 | 0.0425 | 102.5291 | 2.4617 |
| DE0001135267 | 2015-01-04 | 2004-10-27 | 0.0375 | 99.4748 | 0.2869 |
| DE0001135283 | 2015-07-04 | 2005-04-28 | 0.0325 | 95.9702 | 1.8825 |
| DE0001135291 | 2016-01-04 | 2005-10-30 | 0.035 | 97.1815 | 0.2678 |
| DE0001134468 | 2016-06-20 | 1986-06-20 | 0.06 | 114.2849 | 3.7049 |
| DE0001135309 | 2016-07-04 | 2006-04-26 | 0.04 | 100.2847 | 2.3169 |
| DE0001134492 | 2016-09-20 | 1986-09-20 | 0.05625 | 112.23 | 2.0594 |
| DE0001135317 | 2017-01-04 | 2006-10-31 | 0.0375 | 98.397 | 0.2869 |
| DE0001135333 | 2017-07-04 | 2007-04-27 | 0.0425 | 102.0235 | 2.9262 |
| DE0001135341 | 2018-01-04 | 2007-09-21 | 0.04 | 99.8483 | 0.8415 |
| DE0001134922 | 2024-01-04 | 1993-12-29 | 0.0625 | 121.2711 | 0.4781 |
| DE0001135044 | 2027-07-04 | 1997-07-03 | 0.065 | 125.9157 | 3.765 |
| DE0001135069 | 2028-01-04 | 1998-01-04 | 0.05625 | 114.5791 | 0.4303 |
| DE0001135085 | 2028-07-04 | 1998-10-07 | 0.0475 | 103.2202 | 2.7514 |
| DE0001135143 | 2030-01-04 | 2000-01-04 | 0.0625 | 123.4668 | 0.4781 |
| DE0001135176 | 2031-01-04 | 2000-10-27 | 0.055 | 113.4694 | 0.4208 |
| DE0001135226 | 2034-07-04 | 2003-01-22 | 0.0475 | 103.1873 | 2.7514 |
| DE0001135275 | 2037-01-04 | 2004-12-24 | 0.04 | 91.5603 | 0.306 |
| DE0001135325 | 2039-07-04 | 2006-12-28 | 0.0425 | 95.4441 | 4.3081 |