QuantLib 金融计算——案例之主成分久期(PCD)
介绍主成分久期的概念,并用中国市场的数据作为案例。
由于版本问题,代码可能与最新版不兼容。
QuantLib 金融计算——案例之主成分久期(PCD)
概述
关键期限上利率的变动通常有较强的相关性,所以,使用 KRD 天然的存在着“共线性”的隐患。
处理共线性的常见手段是主成分分析(PCA),这也就引出了主成分久期(PCD)的概念——债券价格关于主成分的敏感性。
主成分久期
关于主成分久期的高级内容请见《Interest Rate Risk Modeling》阅读笔记——第十章。
主成分是原始变量的线性组合,可以证明 PCD 也是 KRD 的线性组合,因此计算 PCD 需要分三步:
- 算出关键利率的 KRD;
- 对关键利率做 PCA;
- 根据 KRD 和 PCA 的载荷矩阵(loading)计算 PCD
计算案例
沿用《案例之 KRD、Fisher-Weil 久期及久期的解释能力》的数据,KRD 的计算略过,直接使用最终结果。
利率变化的主成分分析
需要注意的是,这里不需要对数据做标准化(standardize),否则最终计算 KRD 时要做一次尺度变换。但遵照《Interest Rate Risk Modeling》的做法,最终的主成分因子做了归一化(normalize)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import pandas as pd
import statsmodels.api as sm
import seaborn as sns
ratesChg = pd.read_csv(
'ratesChg.csv', parse_dates=True, index_col='date')
returns = pd.read_csv(
'returns.csv', parse_dates=True, index_col='date')
pca = sm.PCA(
ratesChg,
standardize=False,
demean=True,
normalize=True)
print(pca.loadings)
'''
comp_00 comp_01 comp_02 ... comp_11 comp_12 comp_13
1D 0.471356 0.877932 -0.060239 ... 0.015957 0.024632 0.006903
6M 0.047785 0.023852 0.897648 ... -0.001783 0.012518 -0.018913
1Y 0.298379 -0.136045 0.227319 ... -0.132121 -0.011556 -0.044387
2Y 0.310444 -0.149192 0.123286 ... 0.645939 -0.030575 0.140874
3Y 0.342030 -0.157388 0.033696 ... -0.385047 -0.121084 0.023274
4Y 0.342225 -0.187096 0.013315 ... 0.023240 0.393166 -0.008804
5Y 0.303104 -0.174121 0.034038 ... 0.066626 -0.031194 -0.094945
6Y 0.266243 -0.131857 -0.053863 ... -0.499595 -0.316239 -0.183736
7Y 0.224635 -0.120262 -0.054711 ... 0.102571 -0.247733 0.106077
8Y 0.218911 -0.138575 -0.168238 ... -0.150574 0.655571 -0.091769
9Y 0.217848 -0.115892 -0.188426 ... 0.132909 -0.470151 0.134931
10Y 0.136793 -0.117408 -0.208336 ... 0.180370 0.058729 0.088273
15Y 0.135273 -0.106458 -0.087883 ... 0.259897 -0.024268 -0.592554
20Y 0.102095 -0.090580 -0.020611 ... -0.106187 0.108275 0.733208
'''
下面计算一下每个成分因子对回报率的解释能力。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
R2 = pd.DataFrame(
data=[sm.OLS(endog=returns, exog=pca.factors.iloc[:, i]).fit().rsquared for i in range(pca._ncomp)],
index=pca.loadings.columns)
print(R2)
'''
comp_00 0.442932
comp_01 0.098024
comp_02 0.039253
comp_03 0.129587
comp_04 0.035543
comp_05 0.036428
comp_06 0.055197
comp_07 0.000370
comp_08 0.045802
comp_09 0.000013
comp_10 0.004617
comp_11 0.000724
comp_12 0.018448
comp_13 0.000376
'''
上一篇中构造的水平因子的解释能力大约是 50%,而前四个主成分因子的解释能力大约能达到 70%(0.7 = 0.442932 + 0.098024 + 0.039253 + 0.129587)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
pcReg = sm.OLS(
endog=returns, exog=pca.factors).fit()
# print(pcReg.summary())
idx = [0, 1, 2, 3, 4, 5, 6, 8, 10, 12]
pcReg = sm.OLS(
endog=returns, exog=pca.factors.iloc[:, idx]).fit()
print(pcReg.summary())
'''
OLS Regression Results
=======================================================================================
Dep. Variable: return R-squared (uncentered): 0.906
Model: OLS Adj. R-squared (uncentered): 0.902
Method: Least Squares F-statistic: 228.9
Date: Wed, 18 Nov 2020 Prob (F-statistic): 4.81e-116
Time: 15:22:48 Log-Likelihood: 1424.0
No. Observations: 248 AIC: -2828.
Df Residuals: 238 BIC: -2793.
Df Model: 10
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
comp_00 -0.0265 0.001 -33.458 0.000 -0.028 -0.025
comp_01 0.0125 0.001 15.740 0.000 0.011 0.014
comp_02 0.0079 0.001 9.960 0.000 0.006 0.009
comp_03 -0.0143 0.001 -18.097 0.000 -0.016 -0.013
comp_04 -0.0075 0.001 -9.478 0.000 -0.009 -0.006
comp_05 0.0076 0.001 9.595 0.000 0.006 0.009
comp_06 0.0094 0.001 11.811 0.000 0.008 0.011
comp_08 -0.0085 0.001 -10.759 0.000 -0.010 -0.007
comp_10 -0.0027 0.001 -3.416 0.001 -0.004 -0.001
comp_12 0.0054 0.001 6.828 0.000 0.004 0.007
==============================================================================
Omnibus: 130.528 Durbin-Watson: 1.924
Prob(Omnibus): 0.000 Jarque-Bera (JB): 7723.672
Skew: -1.214 Prob(JB): 0.00
'''
从所有主成分因子中筛选掉少数不显著的因子,总的解释能力已达到了 90%。
计算 PCD
根据这里的推导,PCD 向量等于 KRD 向量与载荷矩阵的乘积。
计算 PCD 时有一个的问题需要注意,即载荷向量(载荷矩阵的某列)元素的符号。单纯从 PCA 的角度来看,载荷向量元素的符号不构成一个问题,如果 $l$ 是载荷向量,$-l$ 也能充当载荷向量。但是元素的符号为载荷向量赋予经济含义,具体到利率期限结构的分析来说,通常约定
- 水平因子(h)对应的向量所有元素都必须为正;
- 斜率因子(s)对应的向量在短期限一端为负,在长期限一端为正;
- 曲率因子(c)对应的向量在中间期限为正,在两端为负。
因此,计算 PCD 之前需要调整载荷向量的符号。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
krd = pd.DataFrame(
data=[
-0.00273973, 0.01761345, 0.02607589, 0.06751827, 0.09790298,
0.12608806, 0.15196510, 0.17540198, 0.19649419, 3.12947679,
3.35232738, 0.00000000, 0.00000000, 0.00000000],
index=pca.loadings.index,
columns=['KRD'])
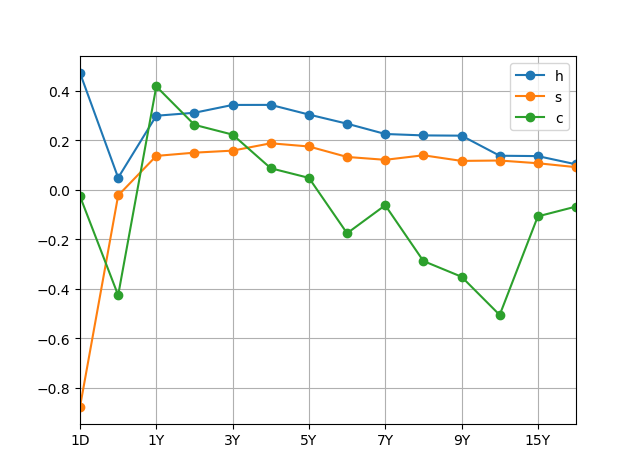
hsc = pca.loadings[['comp_00','comp_01','comp_03']]
hsc.columns = ['h','s','c']
# print(hsc)
hsc.loc[:,'s'] = -hsc.loc[:,'s']
hsc.loc[:,'c'] = -hsc.loc[:,'c']
print(hsc)
hsc.plot(marker='o')
'''
h s c
1D 0.471356 -0.877932 -0.027072
6M 0.047785 -0.023852 -0.426987
1Y 0.298379 0.136045 0.416754
2Y 0.310444 0.149192 0.261607
3Y 0.342030 0.157388 0.222109
4Y 0.342225 0.187096 0.086126
5Y 0.303104 0.174121 0.047247
6Y 0.266243 0.131857 -0.176602
7Y 0.224635 0.120262 -0.063345
8Y 0.218911 0.138575 -0.288706
9Y 0.217848 0.115892 -0.352268
10Y 0.136793 0.117408 -0.506713
15Y 0.135273 0.106458 -0.108318
20Y 0.102095 0.090580 -0.068624
'''
因子的选择其实见仁见智,综合考虑曲线的形状和解释能力,第四个主成分因子更适合做曲率因子。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
pcd = (hsc * krd.values).sum()
print(pcd)
pcdNormalize = pcd * np.sqrt(pca.eigenvals[0:3]).values
print(pcdNormalize)
'''
h 1.657201
s 0.950000
c -2.066973
h 0.026187
s 0.012167
c -0.013483
'''
pcd 是债券关于主成分因子的敏感性,pcdNormalize 是债券关于归一化后主成分的敏感性(和书中的约定一样),可以看出 pcdNormalize 的值和回归系数大体保持一致(注意到符号的转换)。
第一主成分和上一篇的水平因子经济含义相似,但当前得到的 pcd 的值和上一篇中的 Fisher-Weil 久期相去甚远,这主要是因为主成分因子做了尺度缩放。对于水平因子来说,消除尺度缩放
1
2
pcd['h'] * pca.loadings['comp_00'].sum()
# 5.662857296706285
这样第一主成分就变成了利率变动的加权平均,结果与 Fisher-Weil 久期的值接近,且数量级保持一致。