QuantLib 金融计算——随机过程之一般 Black Scholes 过程

由于版本问题，代码可能与最新版不兼容。

QuantLib 金融计算——随机过程之一般 Black Scholes 过程

载入模块

import QuantLib as ql
import pandas as pd
import numpy as np
import seaborn as sn

print(ql.__version__)

1.12

一般 Black Scholes 过程

quantlib-python 中 Black Scholes 框架下常见的几种随机过程均派生自基类 GeneralizedBlackScholesProcess，而 GeneralizedBlackScholesProcess 模拟下列 SDE 描述的一维随机过程：

\[d \ln S_t = \left( r ( t ) - q ( t ) - \frac { \sigma \left( t , S_t \right)^2 } 2 \right) d t + \sigma d W_t\]

等式使用风险中性漂移而不是一般漂移 $\mu$。风险中性利率由股息率 $q(t)$ 调整，并且相应的扩散项是 $\sigma$。

作为基类，GeneralizedBlackScholesProcess 的构造函数为

GeneralizedBlackScholesProcess(x0,
                               dividendTS,
                               riskFreeTS,
                               blackVolTS)

其中：

• x0：QuoteHandle 对象，表示 SDE 的起始值；
• dividendTS：YieldTermStructureHandle 对象，表示股息率的期限结构
• riskFreeTS：YieldTermStructureHandle 对象，表示无风险利率的期限结构
• blackVolTS：BlackVolTermStructureHandle 对象，表示波动率的期限结构

GeneralizedBlackScholesProcess 提供了相应的检查器，返回构造函数接受的关键参数：

• stateVariable；
• dividendYield；
• riskFreeRate；
• blackVolatility

从 StochasticProcess1D 继承来的离散化函数 evolve，描述 SDE 从 $t$ 到 $t + \Delta t$ 的变化。

QuantLib 提供了一些具体的派生类，这些类代表众所周知的具体过程，如

• BlackScholesProcess：没有股息率的一般 BS 过程；
• BlackScholesMertonProcess：一般 BS 过程；
• BlackProcess：一般 Black 过程；
• GarmanKohlagenProcess：包含外汇利率的一般 BS 过程

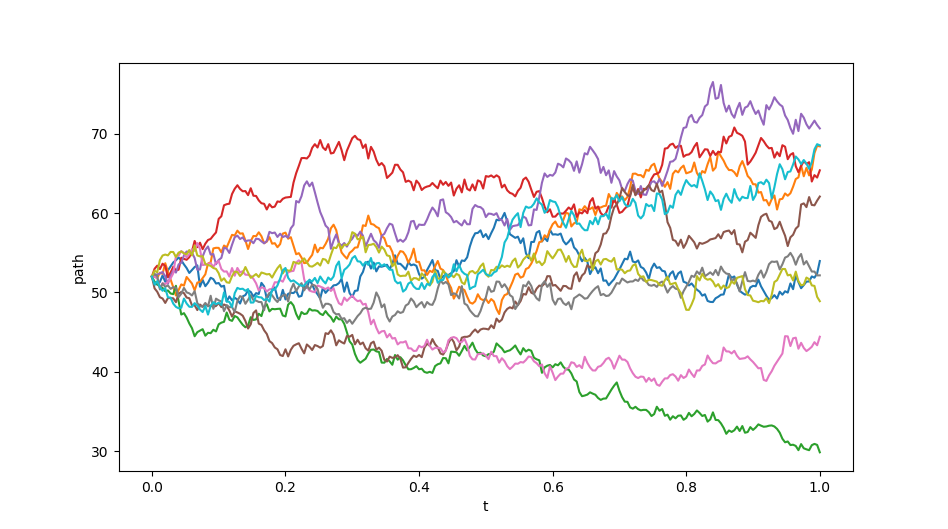
这些派生类在构造和调用方式上大同小异，在下面的例子中，我们将建立一个具有平坦无风险利率、股息率和波动率期限结构的 Black-Scholes-Merton 过程，并画出模拟结果。

def testingStochasticProcesses1():
    refDate = ql.Date(27, ql.January, 2019)
    riskFreeRate = 0.0321
    dividendRate = 0.0128
    spot = 52.0
    vol = 0.2144
    cal = ql.China()
    dc = ql.ActualActual()

    rdHandle = ql.YieldTermStructureHandle(
        ql.FlatForward(refDate, riskFreeRate, dc))
    rqHandle = ql.YieldTermStructureHandle(
        ql.FlatForward(refDate, dividendRate, dc))

    spotQuote = ql.SimpleQuote(spot)
    spotHandle = ql.QuoteHandle(
        ql.SimpleQuote(spot))

    volHandle = ql.BlackVolTermStructureHandle(
        ql.BlackConstantVol(refDate, cal, vol, dc))

    bsmProcess = ql.BlackScholesMertonProcess(
        spotHandle, rqHandle, rdHandle, volHandle)

    seed = 1234
    unifMt = ql.MersenneTwisterUniformRng(seed)
    bmGauss = ql.BoxMullerMersenneTwisterGaussianRng(unifMt)

    dt = 0.004
    numVals = 250

    bsm = pd.DataFrame()

    for i in range(10):
        bsmt = pd.DataFrame(
            dict(
                t=np.linspace(0, dt * numVals, numVals + 1),
                path=np.nan,
                n='p' + str(i)))

        bsmt.loc[0, 'path'] = spotQuote.value()

        x = spotQuote.value()

        for j in range(1, numVals + 1):
            dw = bmGauss.next().value()
            x = bsmProcess.evolve(bsmt.loc[j, 't'], x, dt, dw)
            bsmt.loc[j, 'path'] = x

        bsm = pd.concat([bsm, bsmt])

    sn.lineplot(
        x='t', y='path',
        data=bsm,
        hue='n', legend=None)


testingStochasticProcesses1()