Sobol 序列并行化的实践经验

Sobol 序列并行化的实践经验

随机数发生器并行化的常见策略

随机数发生器的并行化通常有四种策略（文献【1】、【2】）：

1. “随机化”种子
2. 参数化随机数发生器
3. 分块策略
4. 蛙跳策略

“随机化”种子

“随机化”种子就是让每个线程上运行的发生器使用不同的种子，这种策略常见于伪随机数。不过，使用不同随机数种子的发生器所产生的随机数是否依然保持统计意义上的独立性，这一点是未知的。

参数化随机数发生器

某些随机数发生器可以采用不同的参数配置，例如最简单的线性同余发生器，让每个线程运行不同参数配置的发生器就可以实现并行化。不过，这种策略和“随机化”种子有相同的安全隐患，无法确保产生的随机数依然保持统计意义上的独立性。另外，即使保持了独立性，可用的参数配置组合可能数量十分有限，无法充分发挥硬件的并行优势。

分块策略

要确保产生的随机数保持统计意义上的独立性，最简单的办法就是使用一个发生器，在不同的线程上返回不同的数字。要做到这一点可以采用分块生成的策略，下面举个例子。

无论是伪随机还是拟随机，发生器产生的随机数的顺序是不变的。假设要在 4 个线程上并行发生 10000 个随机数，分块策略就是让第 1 个线程返回第 1~2500 个随机数；第 2 个线程返回第 2501~5000 个随机数；第 3 个线程返回第 5001~7500 个随机数；第 4 个线程返回第 7501~10000 个随机数。

分块策略要求发生器必须有一个“长距离跳转”的功能，而且要保证计算成本尽量低。

蛙跳策略

想要使用一个发生器在不同的线程上返回不同的数字，还可以采用“蛙跳”的策略，下面举个例子。

假设要在 4 个线程上并行发生 10000 个随机数，蛙跳策略就是让第 1 个线程返回第 $4k$ 个随机数；第 2 个线程返回第 $4k + 1$ 个随机数；第 3 个线程返回第 $4k + 2$ 个随机数；第 4 个线程返回第 $4k + 3$ 个随机数。

同分块策略相比，每个线程上产生的数字是间隔开的，跳转步长等于线程数。

因为要多次跳转，蛙跳策略要求发生器必须有一个“极低成本”的“短距离跳转”的功能。

Sobol 序列的原理和跳转功能

Sobol 序列的产生依赖于一组事先确定“方向数”——$m$，以及“异或”运算。对于多维 Sobol 序列，每个维度有各自的方向数。

Sobol 序列的发生可以表示为非递归和递归两种形式（文献【1】）：

• 非递归形式：$y_n = g_1 m_1 \oplus g_2 m_2 \oplus g_3 m_3 \oplus \cdots$
• 递归形式：$y_n = y_{n-1} \oplus m_{f(n-1)}, y_0 = 0$

其中 $\oplus$ 表示异或运算；$g_i$ 是 $n$ 的 Gray 码的二进制表示，$n$ 的 Gray 码等于 $n \oplus (n/2)$，而 $n \oplus (n/2) = \dots g_3 g_2 g_1$；$f(n)$ 表示 $n$ 的二进制编码中最右侧的 0 所在的位数。

若采用 32 位整数，$x_n = 2^{-32} y_n$，$x_n$ 就是服从单位均匀分布的 Sobol 序列。

非递归形式表明 Sobol 序列有低成本的长距离跳转功能，因为若采用 32 位整数，直接计算 $y_n$ 至多进行 32 次异或计算。计算 Sobol 序列的程序通常都会提供一个 skipTo 函数，实现长距离跳转。

Sobol 序列并行化实践

随机数的并行化要求精准的操作线程，因此在最常见的“单机多核”情形下可以采用 OpenMP 框架。

分块策略

假设已经具备了单线程上的 Sobol 序列发生器 SobolRsg，可以构造一个复合对象 OmpSobolRsg，内部包含 $N$ 个完全相同的 SobolRsg 对象。在集中调用之前，事先告知 OmpSobolRsg 未来要调用的次数 $M$，将 $N$ 个 SobolRsg 对象分别跳转到合适的位置，第 $i$ 个 SobolRsg 对象将专门在第 $i$ 个线程上调用。这样就实现了 Sobol 序列的并行发生。

借助 OpenMP 框架，上述设计很容易实现，实现细节不赘述。

蛙跳策略

在蛙跳策略下，需要对 SobolRsg 对象稍加改造，以便实现从 $y_{n}$ 直接到 $y_{n+N}$ 的递归。和分块策略类似，需要构造一个复合对象 OmpSobolRsg，内部包含 $N$ 个完全相同的 SobolRsg 对象。无需事先告知未来要调用的次数，只需初始化阶段将 $N$ 个 SobolRsg 对象分别跳转，恰好错开一步。第 $i$ 个 SobolRsg 对象将专门在第 $i$ 个线程上调用。这样就实现了 Sobol 序列的并行发生。

借助 OpenMP 框架，上述设计也很容易实现，实现细节不赘述。

蛙跳策略的计算量分析

回想递归形式，在单线程情况下要生成 $K$ 维的 Sobol 序列，需要进行 $K$ 次整数间的异或计算，以及 $K$ 次浮点数除法计算。蛙跳策略中的跳转则会触发若干次异或计算，当线程数量增多时，势必会增加计算量，削弱并行化的效果。

减少异或计算的技巧

依据递归形式，跳转 $N$ 步的话有如下递归表达式：

\[y_n = y_{n-N} \oplus m_{f(n-N)} \oplus \cdots \oplus m_{f(n-2)} \oplus m_{f(n-1)}\]

在原始情况下，跳转 $N$ 步将发生 $N$ 次异或计算。但根据 $f(n)$ 的定义，$m_{f(n-i)}$ 中可能有不少重合的数字。

与此同时，注意到异或计算的几个性质：

• $a \oplus b = b \oplus a$
• $a \oplus (b \oplus c) = (a \oplus b) \oplus c$
• $a \oplus a = 0$
• $a \oplus 0 = a$
• $0 \oplus 0 = 0$

也就是说，偶数个 $m$ 可以归并为 0，而 0 是可以忽略的。如果某个数字 $m$ 出现了偶数次，可以直接忽略；如果某个数字 $m$ 出现了奇数次，只保留一次就可以了。文献【1】中就举了这样的例子，跳转 $2^p$ 步只需 2 次异或计算。

尽管如此，同分块策略相比蛙跳策略避免不了频繁跳转，也就避免不了多余的异或计算，这可能会导致并行 Monte Carlo 模拟的加速效率大打折扣。

分块策略不算缺点的缺点

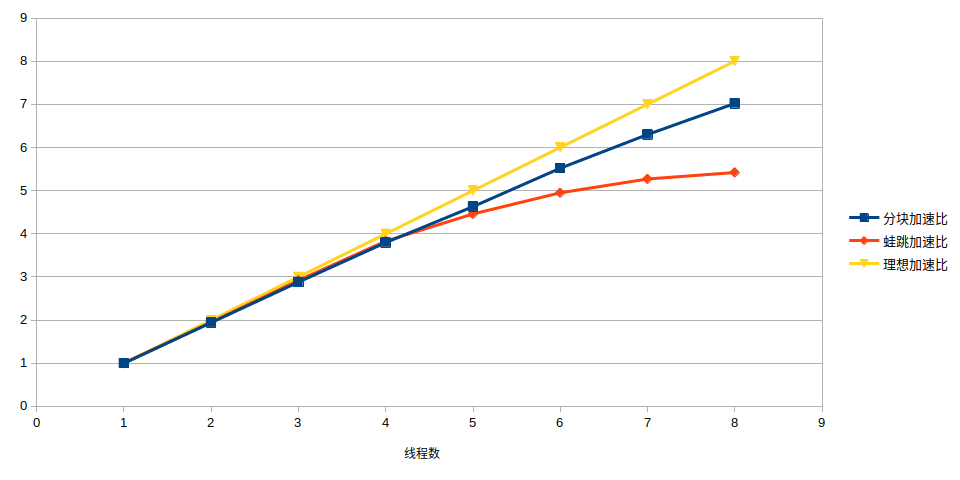
和蛙跳策略相比，分块策略避免了反复跳转，但要求事先告知要调用的次数，这一点和随机数发生器通常的使用模式相背离。但是瑕不掩瑜，分块策略可以获得更好地加速比。笔者分别采用分块和蛙跳策略并行化了 QuantLib 的 Monte Carlo 定价框架，在 8 核 CPU 上，分块策略的加速比在 7 倍左右，而蛙跳策略的加速比在 5.4 倍左右。

图中可以看到，当线程数较少时，两种策略难分伯仲；但当线程数较多时，蛙跳策略的加速效率明显下降，这是频繁跳转造成的拖累。

参考文献

【1】Parallelisation Techniques for Random Number Generators

【2】Tina’s Random Number Generator Library